ABINIT Discussion Forums

There are 2 standard ways to specify the kpoint grid, either with
kptrlatt or with ngkpt (see http://www.abinit.org/documentation/input-variables).
These make a single uniform grid, centered on
gamma, and which is either aligned with the reciprocal space lattice
vectors (ngkpt) or more general (kptrlatt).


Then you add on the shifts, taking the uniform grid and replicating it
once for each shift (so if there is no 0 0 0 shift, then gamma is not
contained in the final set).

Then the grid is reduced to a general kptrlatt lattice, plus some shifts.

In all of the normal cases, and all the Monkhorst Pack grids, and
almost all you ever want to do, it is possible to reduce to a
single-shifted kptrlatt. Often the kptrlatt will not be "orthogonal",
ie not oriented along the reciprocal lattice vectors, but this is not
a problem. In many other codes it is not possible to generate a
"non-orthogonal" grid, even though the MP
specification explicitly creates these grids, in order to get a
uniform density of kpts in cartesian reciprocal space (as opposed to
reduced reciprocal space).

However, you have full freedom to choose kpoints as you wish (you can
also specify them explicitly with nkpt wkpt and kpt). If you set:

ngkpt 6 6 4
nshiftk 2
shiftk
0.5 0.5 0.5
0.33 0.33 0.15

then abinit will not be able to reduce the grid (I just tried, to make
sure), and it is a clear indicator that the grid is not homogeneous in
space. You may have some good reason to do this, but of course the GW
calculations (and others, electron-phonon, etc) do not like this
because they count on being able to use symmetry operations to
complete perturbations and wave functions. If your k grid breaks the
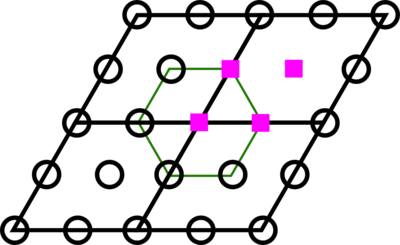
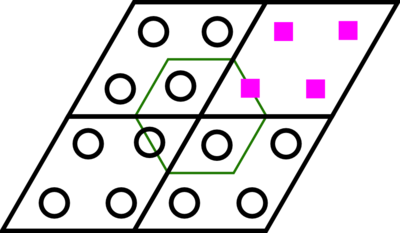
symmetry of the full crystal, this is not possible. This is shown in the following
figures. The unshifted hexagonal 2x2 grid

has 4 pink points in the Brillouin Zone.

In this drawing a 0.5 0.5 shift is applied to the hexagonal grid:

Clearly the second grid has broken the 6-axis of the k-point grid, which is highlighted by the green hexagon.


So to sum up: all the grids you are ever likely to need can be described by a
kptrlatt and a single shift, which is why prtkpt gives you these and
why your inputs are usually reduced to a single shift. But even with a
single shift you are still not guaranteed to respect the symmetries:
you have to choose it appropriately (0.5 0.5 0.5 for cubic, 0 0 0.5
for tetragonal and hexagonal...)

Inhomogeneous and/or targeted kpoint list generation

Dear All,

I wish to calculate optical absorption and optical conductivity of graphene, a semi-metal with zero bandgap at the special K point in the Brillouin Zone. I am having trouble to get physical agreement and as these properties are known to require large number of kpoints, then I wish to generate more kpoints around K, and maybe less anywhere.

1) Is it possible to generate a k-point list with high density in a given region / around a given k-point? I know about the wtk keyword, but I'm not sure if it would do an equivalent job and if so, how to set it.

2) Is it possible to generate a kpt list that contains a specific kpt? (say I want it to contain the point K = 1/3 1/3 0). I know about the kptbounds keyword, but in my understanding it generates a kpt list along a rectilinear path, and I think that for response calculations the wavefunctions (WFK or 1WF) need to be computed through kpts dispersed in the Brillouin Zone.

I am using:

#Definition of the k-point grid
kptopt 1
nshiftk 1
shiftk 0.0 0.0 0.5 ! recommended for Hex lattices
ngkpt 60 60 2 ! SCF WFK converges with 18 18 2

Thanks,
Temok

temok wrote:Inhomogeneous and/or targeted kpoint list generation

Dear All,

I wish to calculate optical absorption and optical conductivity of graphene, a semi-metal with zero bandgap at the special K point in the Brillouin Zone. I am having trouble to get physical agreement and as these properties are known to require large number of kpoints, then I wish to generate more kpoints around K, and maybe less anywhere.

1) Is it possible to generate a k-point list with high density in a given region / around a given k-point? I know about the wtk keyword, but I'm not sure if it would do an equivalent job and if so, how to set it.

you need to be very prudent when setting your kpt grid by hand: you can do so with nkpt kpt and wtk (kptopt 0) but you should make sure that
1) your k-points are a consistent grid, compatible with symmetry
2) your k-point weights are appropriate so you are not weighting some part of the BZ more than others. The best would be a uniform grid (coarse), and near K splitting it into a finer grid (say 2 times finer) with weights divided by 2x2=4 (for 2 dimensions in the plane), such that the weight per unit area stays constant.
Usually people just hit graphene with all the k-points they can muster

2) Is it possible to generate a kpt list that contains a specific kpt? (say I want it to contain the point K = 1/3 1/3 0). I know about the kptbounds keyword, but in my understanding it generates a kpt list along a rectilinear path, and I think that for response calculations the wavefunctions (WFK or 1WF) need to be computed through kpts dispersed in the Brillouin Zone.

I am using:

#Definition of the k-point grid
kptopt 1
nshiftk 1
shiftk 0.0 0.0 0.5 ! recommended for Hex lattices
ngkpt 60 60 2 ! SCF WFK converges with 18 18 2

Thanks,
Temok

If you shift 0 0 in the plane and have a ngkpt which is a multiple of 3, then you will have 1/3 1/3 (or a symmetry-equivalent point) in your grid.

Matthieu

hello,
I would suggest to put these comments about kptrltt in these words in the abinit doc.

Hello
I am using a visual software that generate the input files for abinit (nothing to do with the parameters, everything set visually), but every time I am running it, the simulation failed. So I need to know what is the exact conditions to setup this parameter:
converge SCF energy to ??
I am doing a Single walled carbon nanotubes (10, 10)

Best regards,

Hi jtalia,

I assume you look for a reasonable value for the difference in energy between SCF cycles to stop. There is no recipe here, you should be able to find it by performing a convergence study. Just a guess ... I would say 10^-8 maybe even smaller but look on your actual model at the evolution of the energy.
Curiosity will kill me ... can you disclose the name of that magic visual software that produces Abinit files?

Kind regards,

Alain