k-point generation in ABINIT
Posted: Wed Oct 21, 2009 9:04 pm
There are 2 standard ways to specify the kpoint grid, either with
kptrlatt or with ngkpt (see http://www.abinit.org/documentation/input-variables).
These make a single uniform grid, centered on
gamma, and which is either aligned with the reciprocal space lattice
vectors (ngkpt) or more general (kptrlatt).
Then you add on the shifts, taking the uniform grid and replicating it
once for each shift (so if there is no 0 0 0 shift, then gamma is not
contained in the final set).
Then the grid is reduced to a general kptrlatt lattice, plus some shifts.
In all of the normal cases, and all the Monkhorst Pack grids, and
almost all you ever want to do, it is possible to reduce to a
single-shifted kptrlatt. Often the kptrlatt will not be "orthogonal",
ie not oriented along the reciprocal lattice vectors, but this is not
a problem. In many other codes it is not possible to generate a
"non-orthogonal" grid, even though the MP
specification explicitly creates these grids, in order to get a
uniform density of kpts in cartesian reciprocal space (as opposed to
reduced reciprocal space).
However, you have full freedom to choose kpoints as you wish (you can
also specify them explicitly with nkpt wkpt and kpt). If you set:
ngkpt 6 6 4
nshiftk 2
shiftk
0.5 0.5 0.5
0.33 0.33 0.15
then abinit will not be able to reduce the grid (I just tried, to make
sure), and it is a clear indicator that the grid is not homogeneous in
space. You may have some good reason to do this, but of course the GW
calculations (and others, electron-phonon, etc) do not like this
because they count on being able to use symmetry operations to
complete perturbations and wave functions. If your k grid breaks the
symmetry of the full crystal, this is not possible. This is shown in the following
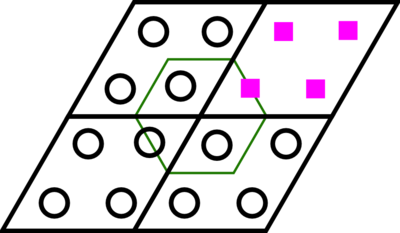
figures. The unshifted hexagonal 2x2 grid
has 4 pink points in the Brillouin Zone.
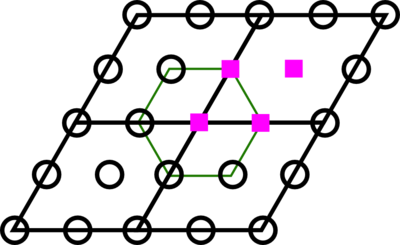
In this drawing a 0.5 0.5 shift is applied to the hexagonal grid:
Clearly the second grid has broken the 6-axis of the k-point grid, which is highlighted by the green hexagon.
So to sum up: all the grids you are ever likely to need can be described by a
kptrlatt and a single shift, which is why prtkpt gives you these and
why your inputs are usually reduced to a single shift. But even with a
single shift you are still not guaranteed to respect the symmetries:
you have to choose it appropriately (0.5 0.5 0.5 for cubic, 0 0 0.5
for tetragonal and hexagonal...)
kptrlatt or with ngkpt (see http://www.abinit.org/documentation/input-variables).
These make a single uniform grid, centered on
gamma, and which is either aligned with the reciprocal space lattice
vectors (ngkpt) or more general (kptrlatt).
Then you add on the shifts, taking the uniform grid and replicating it
once for each shift (so if there is no 0 0 0 shift, then gamma is not
contained in the final set).
Then the grid is reduced to a general kptrlatt lattice, plus some shifts.
In all of the normal cases, and all the Monkhorst Pack grids, and
almost all you ever want to do, it is possible to reduce to a
single-shifted kptrlatt. Often the kptrlatt will not be "orthogonal",
ie not oriented along the reciprocal lattice vectors, but this is not
a problem. In many other codes it is not possible to generate a
"non-orthogonal" grid, even though the MP
specification explicitly creates these grids, in order to get a
uniform density of kpts in cartesian reciprocal space (as opposed to
reduced reciprocal space).
However, you have full freedom to choose kpoints as you wish (you can
also specify them explicitly with nkpt wkpt and kpt). If you set:
ngkpt 6 6 4
nshiftk 2
shiftk
0.5 0.5 0.5
0.33 0.33 0.15
then abinit will not be able to reduce the grid (I just tried, to make
sure), and it is a clear indicator that the grid is not homogeneous in
space. You may have some good reason to do this, but of course the GW
calculations (and others, electron-phonon, etc) do not like this
because they count on being able to use symmetry operations to
complete perturbations and wave functions. If your k grid breaks the
symmetry of the full crystal, this is not possible. This is shown in the following
figures. The unshifted hexagonal 2x2 grid
has 4 pink points in the Brillouin Zone.
In this drawing a 0.5 0.5 shift is applied to the hexagonal grid:
Clearly the second grid has broken the 6-axis of the k-point grid, which is highlighted by the green hexagon.
So to sum up: all the grids you are ever likely to need can be described by a
kptrlatt and a single shift, which is why prtkpt gives you these and
why your inputs are usually reduced to a single shift. But even with a
single shift you are still not guaranteed to respect the symmetries:
you have to choose it appropriately (0.5 0.5 0.5 for cubic, 0 0 0.5
for tetragonal and hexagonal...)