ABINIT Discussion Forums

Hi,

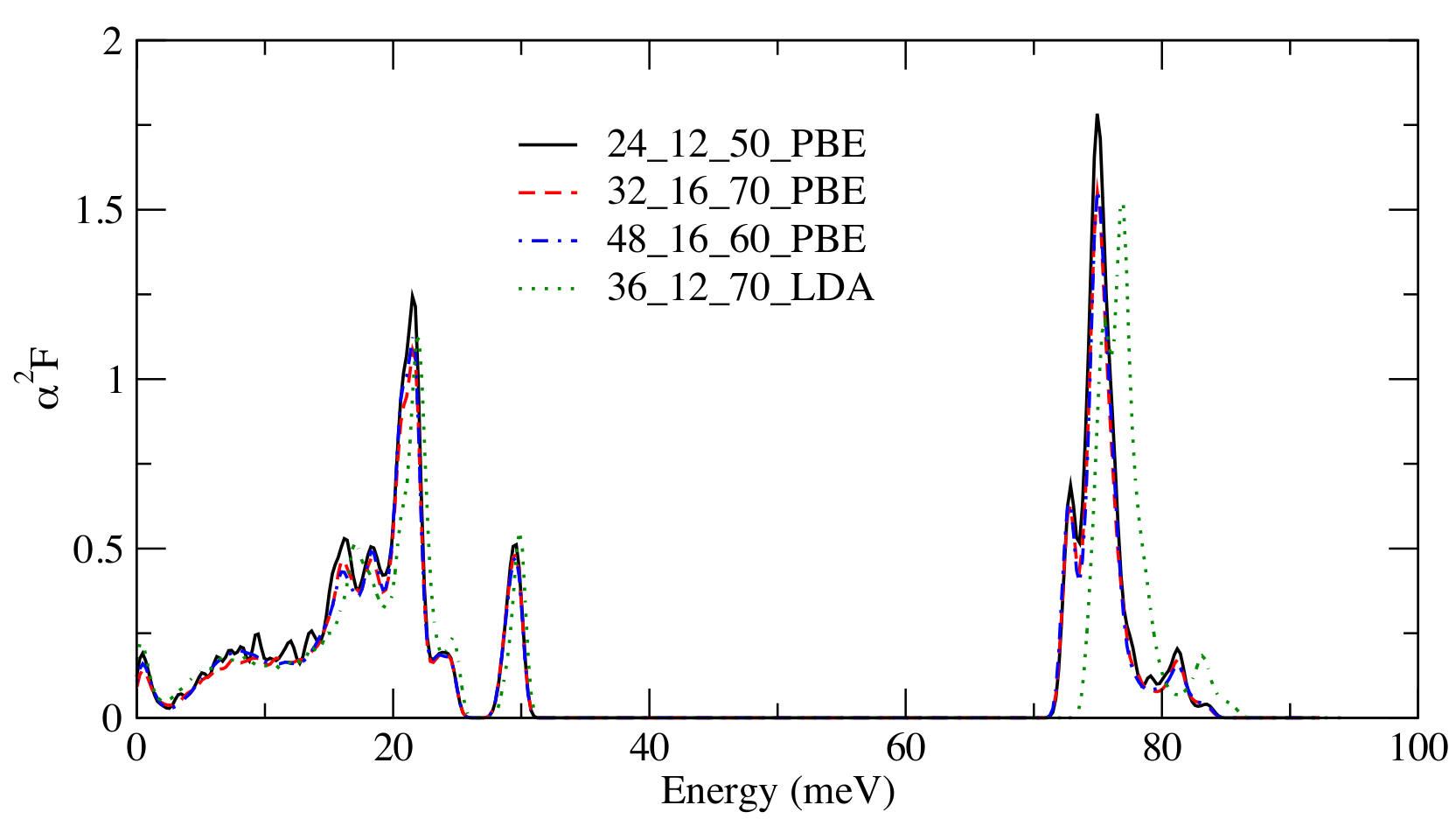
I am calculating the electron-phonon coupling (EPC) in certain 2D materials (MXenes). I have encountered a problem concerning divergences of the EPC at low energies, due to the Eliashberg function not going to zero for zero energy. After application of the acoustic sum rule (ASR), the phonon band structure is completely fine, without negative values. The phonon DOS, however, does not go exactly to zero, which seems to be the root cause of the problem. I would assume that the phonon DOS is calculated from the eigenvalues after correction with the ASR, so I also don't clearly understand why this is the case. Moreover, both gaussian and tetrahedron integration produce this issue.

The issue can be clearly seen in the following Eliashberg function, extracted from the A2F file:



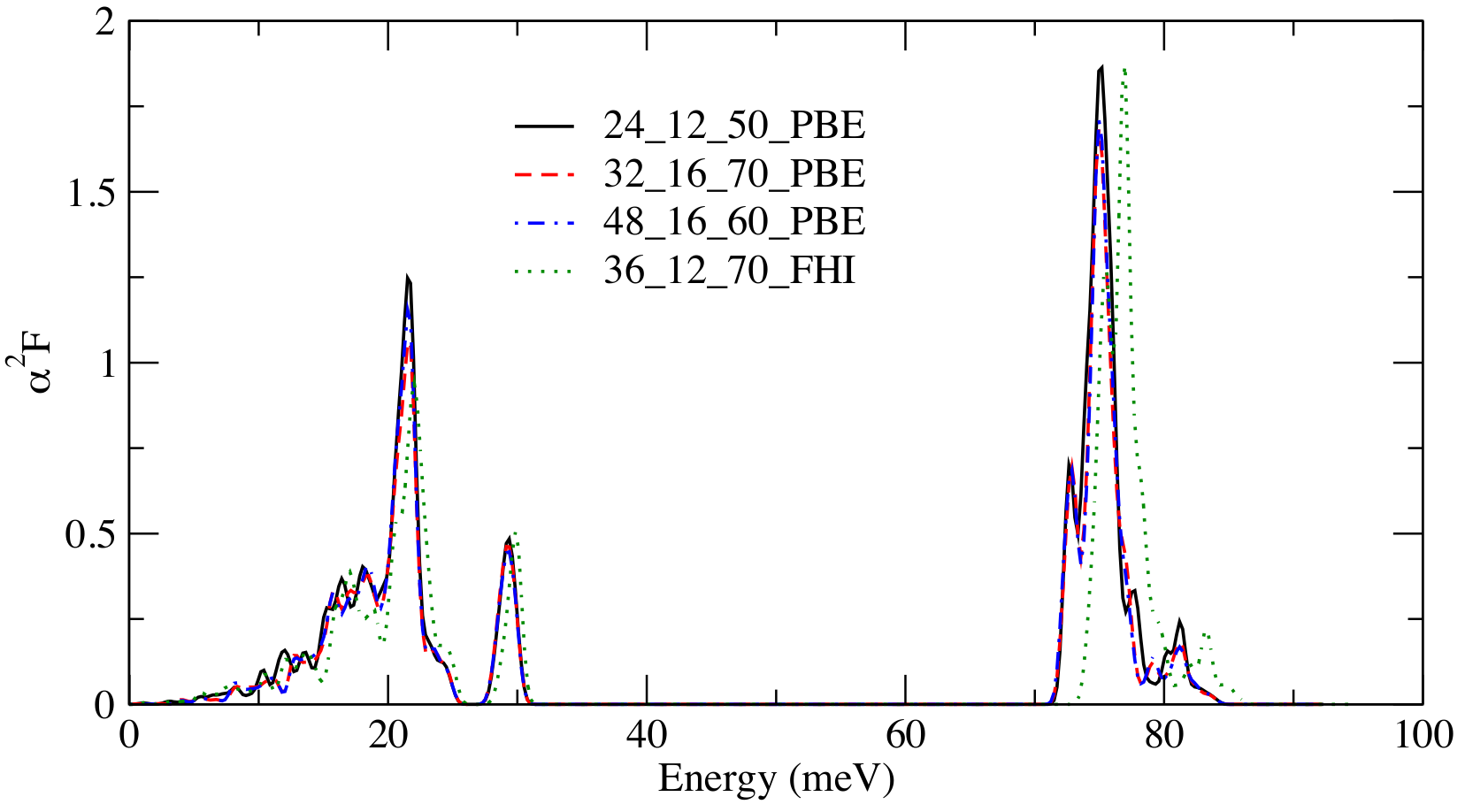
However, the Eliashberg function from the A2F_QGRID file is very different at low energies and doesn't show this problem:



This Eliashberg function is perfectly suited to extract the isotropic EPC. However, I would like to understand better how one arrives at these very different results.

Hence my question: Does anyone know the difference in calculation between those two versions of the Eliashberg function outputted by anaddb? I haven't been able to find documentation on the topic. As you can see in the figures, the issue is robust against variations in the k-point grid, q-point grid, the ecut and the functional (listed in this order in the quadruplets given as insets in the graphs above).

Best wishes,
Jonas

Hi Jonas,

very interesting topic!

For the Gaussian case, it can come from the pileup of the gaussian tails, which do not go strictly to 0 at 0 frequency, even if there are no low lying eigenvalues in the phonon spectrum

Given you have checked for this (tetrahedron + QGRID) I suspect you are getting _true_ interpolated low lying frequencies. MXenes are basically 2D materials, in which you will get parabolic phonon bands, and an accumulation of DOS at low omega, compared to a true 3D crystal with linear dispersion near q=0. This parabolic dispersion is very delicate: abinit does not impose the rotational sum rule perfectly, so it might be a) a bit too linear instead of parabolic for a real 2D system or b) slightly too low in a 3D stacked system (MAX) if the phonon band interpolation does not do a perfect job. At any rate for a real 2D system the DOS does not go as omega^2 for low frequencies, so you have to be careful. Let's see your phonon band structure, and also check points away from the high symmetry lines: these may give the accumulation in the DOS and be invisible in the BS.

don't hesitate to write me directly.

tot ziens