Elastic and piezoelectric properties with Abinit and AbiPy

Elastic and piezoelectric properties with Abinit and AbiPy#

This tutorial shows how to calculate the following physical properties related to strain:

the clamped-ion elastic tensor
the clamped-ion piezoelectric tensor (insulators only)
the internal strain tensor
the atomic relaxation corrections to the elastic and piezoelectric tensor (relaxed-ion tensors)

The discussion is based on the tutorial on elastic properties available on the Abinit web site. More specifically, we will discuss how to

build a flow to compute all the ingredients needed for elastic and piezoelectric tensors
use anaddb and AbiPy to obtain the tensors and compute several important physical properties starting from the final DDB file produced by the flow
perform a convergence study with respect to the k-mesh and use the DdbRobot to analyze the convergence.

You might find additional material related to the present section in the following references (already mentioned in the official tutorial):

The first paper provides a detailed discussion of the theory underlying the incorporation of atom-relaxation corrections. We strongly recommend to read this article as this notebook will mainly focus on the usage of the python API assuming you are already familiar with the theoretical aspects. The second paper discusses in more details the DFPT treatment of strain perturbations in Abinit.

If you are already familiar with python and AbiPy-Abinit are already installed and configured, you may want to use directly the command line interface. There is a README.md file in the directory of this lesson explaining how to analyze the data from the shell using ipython and matplotlib.

Note

The code in this notebook requires abinit >= 8.9 and abipy >= 0.6

DFPT calculation of elastic and piezolectric tensors#

Before starting, we need to import the python modules and the functions needed in the notebook:

import numpy as np
import warnings
warnings.filterwarnings("ignore") # to get rid of deprecation warnings

from abipy import abilab
abilab.enable_notebook() # This line tells AbiPy we are running inside a notebook
import abipy.flowtk as flowtk

# This line configures matplotlib to show figures embedded in the notebook.
# Replace `inline` with `notebook` in classic notebook
%matplotlib inline

# Option available in jupyterlab. See https://github.com/matplotlib/jupyter-matplotlib
#%matplotlib widget

and an useful function from the lesson_elastic module required to generate our DFPT flows:

from lesson_elastic import make_scf_input
abilab.print_source(make_scf_input)

def make_scf_input(ngkpt=(4, 4, 4)):
    """
    This function constructs the input file for the GS calculation of
    AlAs in hypothetical wurzite (hexagonal) structure.
    In principle, the stucture should be relaxed before starting the calculation,
    here we use the *unrelaxed* geometry of the official tutorial.

    Args:
        ngkpt: K-mesh used both in the GS and in the DFPT part.
    """

    # Initialize structure. Use enough significant digits
    # so that Abinit will recognize the correct spacegroup
    # (Hexagonal and rhombohedral lattices are a bit problematic).
    structure = abilab.Structure.from_abivars(
        acell=[7.5389648144E+00, 7.5389648144E+00, 1.2277795374E+01],
        natom=4,
        ntypat=2,
        rprim=[ np.sqrt(0.75), 0.5, 0.0 ,
               -np.sqrt(0.75), 0.5, 0.0,
                          0.0, 0.0, 1.0],
        typat=[1, 1, 2, 2],
        xred=[1/3, 2/3, 0,
              2/3, 1/3, 1/2,
              1/3, 2/3, 3.7608588373E-01,
              2/3, 1/3, 8.7608588373E-01],
        znucl=[13, 33],
    )

    pseudos = abidata.pseudos("13al.pspnc", "33as.pspnc")
    gs_inp = abilab.AbinitInput(structure, pseudos=pseudos)

    # Set other important variables (consistent with tutorial)
    # All the other DFPT runs will inherit these parameters.
    gs_inp.set_vars(
        nband=8,
        ecut=6.0,
        ecutsm=0.5,        # Important when performing structural optimization
                           # with variable cell. All DFPT calculations should use
                           # the same value to be consistent.
        ngkpt=ngkpt,
        nshiftk=1,
        shiftk=[0.0, 0.0, 0.5],   # This choice preserves the hexagonal symmetry of the grid.
        diemac=9.0,
        nstep=40,
        paral_kgb=0,
        tolvrs=1.0e-18,
    )

    return gs_inp

The function makes some assumptions for important parameters such as the crystalline structure and the pseudos. This is done on purpose to keep the code as simple as possible. It should not be so difficult to generalize the implementation to take into account other cases. Note how the function accepts an optional argument ngkpt defining the k-mesh so that we can easily change the sampling e.g. for convergence studies.

Let’s start to play with our new function:

scf_input = make_scf_input()
scf_input

##############################################
#### SECTION: basic
##############################################
nband 8
ecut 6.0
ngkpt 4 4 4
nshiftk 1
shiftk 0.0 0.0 0.5
nstep 40
tolvrs 1e-18
##############################################
#### SECTION: files
##############################################
indata_prefix indata/in
tmpdata_prefix tmpdata/tmp
outdata_prefix outdata/out
pp_dirpath /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/abipy/data/pseudos
pseudos 13al.pspnc 33as.pspnc
##############################################
#### SECTION: gstate
##############################################
diemac 9.0
##############################################
#### SECTION: paral
##############################################
paral_kgb 0
##############################################
#### SECTION: rlx
##############################################
ecutsm 0.5
##############################################
#### STRUCTURE
##############################################
natom 4
ntypat 2
typat
1 1 2
2
znucl 13 33
xred
0.3333333333 0.6666666667 0.0000000000
0.6666666667 0.3333333333 0.5000000000
0.3333333333 0.6666666667 0.3760858837
0.6666666667 0.3333333333 0.8760858837
acell 1.0 1.0 1.0
rprim
6.5289350475 3.7694824072 0.0000000000
-6.5289350475 3.7694824072 0.0000000000
0.0000000000 0.0000000000 12.2777953740

print(scf_input.structure)

Full Formula (Al2 As2)
Reduced Formula: AlAs
abc   :   3.989448   3.989448   6.497130
angles:  90.000000  90.000000 120.000000
pbc   :       True       True       True
Sites (4)
  #  SP           a         b         c
---  ----  --------  --------  --------
  0  Al    0.333333  0.666667  0
  1  Al    0.666667  0.333333  0.5
  2  As    0.333333  0.666667  0.376086
  3  As    0.666667  0.333333  0.876086

scf_input.structure.plot();

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/IPython/core/formatters.py:343, in BaseFormatter.__call__(self, obj)
    341     pass
    342 else:
--> 343     return printer(obj)
    344 # Finally look for special method names
    345 method = get_real_method(obj, self.print_method)

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/IPython/core/pylabtools.py:170, in print_figure(fig, fmt, bbox_inches, base64, **kwargs)
    167     from matplotlib.backend_bases import FigureCanvasBase
    168     FigureCanvasBase(fig)
--> 170 fig.canvas.print_figure(bytes_io, **kw)
    171 data = bytes_io.getvalue()
    172 if fmt == 'svg':

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/backend_bases.py:2175, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2172     # we do this instead of `self.figure.draw_without_rendering`
   2173     # so that we can inject the orientation
   2174     with getattr(renderer, "_draw_disabled", nullcontext)():
-> 2175         self.figure.draw(renderer)
   2176 if bbox_inches:
   2177     if bbox_inches == "tight":

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/artist.py:95, in _finalize_rasterization.<locals>.draw_wrapper(artist, renderer, *args, **kwargs)
     93 @wraps(draw)
     94 def draw_wrapper(artist, renderer, *args, **kwargs):
---> 95     result = draw(artist, renderer, *args, **kwargs)
     96     if renderer._rasterizing:
     97         renderer.stop_rasterizing()

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/artist.py:72, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     69     if artist.get_agg_filter() is not None:
     70         renderer.start_filter()
---> 72     return draw(artist, renderer)
     73 finally:
     74     if artist.get_agg_filter() is not None:

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/figure.py:3162, in Figure.draw(self, renderer)
   3159             # ValueError can occur when resizing a window.
   3161     self.patch.draw(renderer)
-> 3162     mimage._draw_list_compositing_images(
   3163         renderer, self, artists, self.suppressComposite)
   3165     renderer.close_group('figure')
   3166 finally:

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/image.py:132, in _draw_list_compositing_images(renderer, parent, artists, suppress_composite)
    130 if not_composite or not has_images:
    131     for a in artists:
--> 132         a.draw(renderer)
    133 else:
    134     # Composite any adjacent images together
    135     image_group = []

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/matplotlib/artist.py:72, in allow_rasterization.<locals>.draw_wrapper(artist, renderer)
     69     if artist.get_agg_filter() is not None:
     70         renderer.start_filter()
---> 72     return draw(artist, renderer)
     73 finally:
     74     if artist.get_agg_filter() is not None:

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/mpl_toolkits/mplot3d/axes3d.py:441, in Axes3D.draw(self, renderer)
    437 zorder_offset = max(axis.get_zorder()
    438                     for axis in self._axis_map.values()) + 1
    439 collection_zorder = patch_zorder = zorder_offset
--> 441 for artist in sorted(collections_and_patches,
    442                      key=lambda artist: artist.do_3d_projection(),
    443                      reverse=True):
    444     if isinstance(artist, mcoll.Collection):
    445         artist.zorder = collection_zorder

File /usr/share/miniconda/envs/abipy/lib/python3.12/site-packages/mpl_toolkits/mplot3d/axes3d.py:442, in Axes3D.draw.<locals>.<lambda>(artist)
    437 zorder_offset = max(axis.get_zorder()
    438                     for axis in self._axis_map.values()) + 1
    439 collection_zorder = patch_zorder = zorder_offset
    441 for artist in sorted(collections_and_patches,
--> 442                      key=lambda artist: artist.do_3d_projection(),
    443                      reverse=True):
    444     if isinstance(artist, mcoll.Collection):
    445         artist.zorder = collection_zorder

AttributeError: 'Arrow3D' object has no attribute 'do_3d_projection'

<Figure size 640x480 with 1 Axes>

We are using the same norm-conserving pseudopotentials of the official tutorial but this does not mean you should use them for production calculations (there must be a reason why the directory is called Psps_for_tests).

There are 16 valence electrons per unit cell hence nband has been set to 8 (yes, we are dealing with a non-magnetic semiconductor):

for pseudo in scf_input.pseudos:
    print(pseudo, "\n")

<NcAbinitPseudo: 13al.pspnc>
  summary: Troullier-Martins psp for element  Al        Thu Oct 27 17:31:05 EDT 1994
  number of valence electrons: 3.0
  maximum angular momentum: d
  angular momentum for local part: d
  XC correlation: LDA_XC_TETER93
  supports spin-orbit: False
  radius for non-linear core correction: 2.09673076353074
  hint for low accuracy: ecut: 0.0, pawecutdg: 0.0
  hint for normal accuracy: ecut: 0.0, pawecutdg: 0.0
  hint for high accuracy: ecut: 0.0, pawecutdg: 0.0 

<NcAbinitPseudo: 33as.pspnc>
  summary: Troullier-Martins psp for element  As        Thu Oct 27 17:37:14 EDT 1994
  number of valence electrons: 5.0
  maximum angular momentum: p
  angular momentum for local part: p
  XC correlation: LDA_XC_TETER93
  supports spin-orbit: False
  radius for non-linear core correction: 2.0573171556401
  hint for low accuracy: ecut: 0.0, pawecutdg: 0.0
  hint for normal accuracy: ecut: 0.0, pawecutdg: 0.0
  hint for high accuracy: ecut: 0.0, pawecutdg: 0.0 

The scf_input represents the building block for our DFPT calculation. As usual, AbiPy provides a Work to compute elastic and piezoelectric properties starting from an input representing a ground-state calculation thus it is just a matter of calling make_scf_input and pass the result to ElasticWork.from_scf_input to construct our flow.

Let’s have a look at the actual implementation:

from lesson_elastic import build_flow
abilab.print_source(build_flow)

def build_flow(options=None):
    """
    Create a `Flow` for phonon calculations. The flow has one work with:

        - 1 GS Task
        - 3 DDK Task
        - 4 Phonon Tasks (Gamma point)
        - 6 Elastic tasks (3 uniaxial + 3 shear strain)

    The Phonon tasks and the elastic task will read the 3 DDK files produced at the beginning
    """
    workdir = options.workdir if (options and options.workdir) else "flow_elastic"

    flow = flowtk.Flow(workdir=workdir)

    # Build input for GS calculation and register the first work.
    scf_input = make_scf_input()

    # Build work for elastic properties (clamped-ions)
    # activate internal strain and piezoelectric part.
    elast_work = flowtk.ElasticWork.from_scf_input(scf_input, with_relaxed_ion=True, with_piezo=True)

    flow.register_work(elast_work)

    return flow

Now we can call the function to build our flow:

flow = build_flow()
flow.show_info()

<Flow, node_id=122, workdir=flow_elastic>
Number of works: 1, total number of tasks: 14
Number of tasks with a given class:

Task Class      Number
------------  --------
ScfTask              1
DdkTask              3
PhononTask           4
ElasticTask          6

and use the get_graphviz method to visualize the connection among the Tasks:

flow.get_graphviz()

../_images/1f6568cef738803527f29d2432e701f7ad347799d7ba353f5370c091a66261aa.svg

# matplotlib version based on networkx
#flow.plot_networkx(with_edge_labels=True);

In a nutshell:

we compute the WFK file in the ScfTask (red circle)
the ground-state wavefunctions are used by the three DdkTasks to compute \(\dfrac{\partial u}{\partial{\bf k}}\) for the three different directions.
The ElasticTasks needs the WFK file to compute the six strain perturbations (3 for uniaxial and 3 for shear strain) while the DDK files are required to compute the mixed 2nd-order derivatives with respect to strain and electric field needed for the piezoelectric tensor.

Note that, contrarily to the approach used in the standard tutorial, the AbiPy Work does not use datasets. The perturbations of interest (strain, atomic-perturbation, ddk, electric field) are obtained with different Tasks that can be executed in parallel.

To understand better this point, we can print a table with the most important Abinit variables defining the DFPT calculation. If the variable is not present in the input, the entry is set to None.

flow.get_vars_dataframe("qpt", "rfphon", "rfatpol", "rfdir", "rfelfd", "rfstrs", "kptopt")

	qpt	rfphon	rfatpol	rfdir	rfelfd	rfstrs	kptopt	class
w0_t0	None	None	None	None	None	None	None	ScfTask
w0_t1	(0, 0, 0)	None	None	(1, 0, 0)	2	None	2	DdkTask
w0_t2	(0, 0, 0)	None	None	(0, 1, 0)	2	None	2	DdkTask
w0_t3	(0, 0, 0)	None	None	(0, 0, 1)	2	None	2	DdkTask
w0_t4	(0, 0, 0)	1	[1, 1]	[1, 0, 0]	None	None	2	PhononTask
w0_t5	(0, 0, 0)	1	[1, 1]	[0, 0, 1]	None	None	2	PhononTask
w0_t6	(0, 0, 0)	1	[3, 3]	[1, 0, 0]	None	None	2	PhononTask
w0_t7	(0, 0, 0)	1	[3, 3]	[0, 0, 1]	None	None	2	PhononTask
w0_t8	(0, 0, 0)	None	None	[1, 0, 0]	None	1	2	ElasticTask
w0_t9	(0, 0, 0)	None	None	[0, 1, 0]	None	1	2	ElasticTask
w0_t10	(0, 0, 0)	None	None	[0, 0, 1]	None	1	2	ElasticTask
w0_t11	(0, 0, 0)	None	None	[1, 0, 0]	None	2	2	ElasticTask
w0_t12	(0, 0, 0)	None	None	[0, 1, 0]	None	2	2	ElasticTask
w0_t13	(0, 0, 0)	None	None	[0, 0, 1]	None	2	2	ElasticTask

If the meaning of these variables is not clear, you can consult the Abinit documentation or access the documentation directly from python with e.g.:

abilab.docvar("rfstrs")

Default value:

0

Description

Used to run strain response-function calculations (e.g. needed to get elastic constants). Define, with rfdir, the set of perturbations. * 0 --> no strain perturbation * 1 --> only uniaxial strain(s) (ipert=natom+3 is activated) * 2 --> only shear strain(s) (ipert=natom+4 is activated) * 3 --> both uniaxial and shear strain(s) (both ipert=natom+3 and ipert=natom+4 are activated) See the possible restrictions on the use of strain perturbations, in the help:respfn.

Note

For your convenience the links to the doc of the different variables are listed below:

Now we can generate the flow_elastic directory with the input files by executing the lesson_elastic.py script. Then use the abirun.py script to launch the entire calculation with:

abirun.py flow_elastic scheduler

You will see that all PhononTasks and ElasticTasks are executed in parallel on your machine once the three DdkTasks are completed.

Warning

Please make sure that AbiPy is properly configured by running:

abicheck.py --with-flow

before executing this tutorial.

To create a manager.yml and scheduler.yml file for your particular machine/installation, please consult this page.

If you prefer to skip this part, you may want to jump to next section about the post-processing of the results. Note that the output files are already available in the repository so it is also possible to try the AbiPy post-processing tools without having to run the flow.

Post-processing the results#

Our flow is completed and we have the final DDB file in the outdata directory of the Work (AbiPy has automatically merged all the partial DDB files at the end of the calculation by invoking anaddb for you). Let’s open this DDB file with:

ddb = abilab.abiopen("flow_elastic/w0/outdata/out_DDB")
print(ddb)

================================= File Info =================================
Name: out_DDB
Directory: /home/runner/work/abipy_book/abipy_book/abipy_book/elastic/flow_elastic/w0/outdata
Size: 27.03 kB
Access Time: Sun Oct 27 17:42:03 2024
Modification Time: Sun Oct 27 17:38:46 2024
Change Time: Sun Oct 27 17:38:46 2024

================================= Structure =================================
Full Formula (Al2 As2)
Reduced Formula: AlAs
abc   :   3.989448   3.989448   6.497130
angles:  90.000000  90.000000 120.000000
pbc   :       True       True       True
Sites (4)
  #  SP           a         b         c  cartesian_forces
---  ----  --------  --------  --------  -------------------------------------------------
  0  Al    0.333333  0.666667  0         [-0.00000000e+00 -0.00000000e+00  4.06423231e-06]
  1  Al    0.666667  0.333333  0.5       [-0.00000000e+00 -0.00000000e+00  4.06423231e-06]
  2  As    0.333333  0.666667  0.376086  [-0.00000000e+00 -0.00000000e+00 -4.06423231e-06]
  3  As    0.666667  0.333333  0.876086  [-0.00000000e+00 -0.00000000e+00 -4.06423231e-06]

Abinit Spacegroup: spgid: 0, num_spatial_symmetries: 12, has_timerev: True, symmorphic: True

================================== DDB Info ==================================

Number of q-points in DDB: 1
guessed_ngqpt: [1 1 1] (guess for the q-mesh divisions made by AbiPy)
ecut = 6.000000, ecutsm = 0.500000, nkpt = 8, nsym = 12, usepaw = 0
nsppol 1, nspinor 1, nspden 1, ixc = 1, occopt = 1, tsmear = 0.010000

Has total energy: True
Total energy: -551.6004805663522 eV
Has forces: True

Cartesian stress tensor in GPa with pressure: -1.518e-07 (GPa):
[[-1.11784777e-05  0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00 -1.11786387e-05  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  2.28125046e-05]]

Has (at least one) atomic pertubation: True
Has (at least one diagonal) electric-field perturbation: False
Has (at least one) Born effective charge: True
Has (all) strain terms: True
Has (all) internal strain terms: True
Has (all) piezoelectric terms: True
Has (all) dynamical quadrupole terms: False

The DdbFile object provides an easy-to-use interface that invokes anaddb to post-process the data stored in the DDB file. All the methods that invoke anaddb use the ana prefix so it is not strange to see that we can obtain the elastic and piezoelectric tensors by just calling:

edata = ddb.anaget_elastic(verbose=1)

ANADDB INPUT:
  outdata_prefix "outdata/out"
 asr 2
 chneut 1
 dieflag 0
 elaflag 3
 piezoflag 3
 instrflag 1
workdir: /tmp/tmpsuvqtekr

Note that we are calling the method without arguments. This means that AbiPy will try to detect automatically how to set the anaddb input variables. The docstring of the method explains the logic used to set the variables.

abilab.print_doc(ddb.anaget_elastic)

    def anaget_elastic(self, relaxed_ion="automatic", piezo="automatic",
                       dde=False, stress_correction=False, asr=2, chneut=1,
                       mpi_procs=1, workdir=None, manager=None, verbose=0, retpath=False, return_input=False):
        """
        Call anaddb to compute elastic and piezoelectric tensors. Require DDB with strain terms.

        By default, this method sets the anaddb input variables automatically
        by looking at the 2nd-order derivatives available in the DDB file.
        This behaviour can be changed by setting explicitly the value of:
        `relaxed_ion` and `piezo`.

        Args:
            relaxed_ion: Activate computation of relaxed-ion tensors.
                Allowed values are [True, False, "automatic"]. Defaults to "automatic".
                In "automatic" mode, relaxed-ion tensors are automatically computed if
                internal strain terms and phonons at Gamma are present in the DDB.
            piezo: Activate computation of piezoelectric tensors.
                Allowed values are [True, False, "automatic"]. Defaults to "automatic".
                In "automatic" mode, piezoelectric tensors are automatically computed if
                piezoelectric terms are present in the DDB.
                NB: relaxed-ion piezoelectric requires the activation of `relaxed_ion`.
            dde: if True, dielectric tensors will be calculated.
            stress_correction: Calculate the relaxed ion elastic tensors, considering
                the stress left inside cell. The DDB must contain the stress tensor.
            asr: Anaddb input variable. See official documentation.
            chneut: Anaddb input variable. See official documentation.
            mpi_procs: Number of MPI processes to use.
            workdir: Working directory. If None, a temporary directory is created.
            manager: |TaskManager| object. If None, the object is initialized from the configuration file
            verbose: verbosity level. Set it to a value > 0 to get more information
            retpath: True to return path to anaddb.nc file.
            return_input: True if the |AnaddbInput| object should be returned as 2nd argument

        Return:
            |ElasticData| object if ``retpath`` is None else absolute path to anaddb.nc file.
        """

Let’s print the object to get a summary of the most important results:

print(edata)

================================= Structure =================================
Full Formula (Al2 As2)
Reduced Formula: AlAs
abc   :   3.989448   3.989448   6.497130
angles:  90.000000  90.000000 120.000000
pbc   :       True       True       True
Sites (4)
  #  SP           a         b         c
---  ----  --------  --------  --------
  0  Al    0.333333  0.666667  0
  1  Al    0.666667  0.333333  0.5
  2  As    0.333333  0.666667  0.376086
  3  As    0.666667  0.333333  0.876086

============================== Anaddb Variables ==============================
{
  "asr": 2,
  "chneut": 1,
  "dieflag": 0,
  "elaflag": 3,
  "instrflag": 1,
  "piezoflag": 3
}

========================= elastic tensors available =========================
[ELASTIC_RELAXED]
relaxed-ion elastic tensor in Voigt notation (shape: (6, 6))
Units: GPa, set to zero below: 0.001, fit_to_structure: True

            xx          yy          zz        yz         xz         xy
xx  135.262182   54.450376   38.052927   0.00000   0.000000   0.000000
yy   54.450376  135.262181   38.052927   0.00000   0.000000   0.000000
zz   38.052927   38.052926  148.211029   0.00000   0.000000   0.000000
yz    0.000000    0.000000    0.000000  30.55071   0.000000   0.000000
xz    0.000000    0.000000    0.000000   0.00000  30.550709   0.000000
xy    0.000000    0.000000    0.000000   0.00000   0.000000  40.405903

[ELASTIC_CLAMPED]
clamped-ion elastic tensor in Voigt notation (shape: (6, 6))
Units: GPa, set to zero below: 0.001, fit_to_structure: True

            xx          yy          zz         yz         xz         xy
xx  165.988592   40.464803   21.090298   0.000000   0.000000   0.000000
yy   40.464802  165.988592   21.090299   0.000000   0.000000   0.000000
zz   21.090298   21.090298  182.585743   0.000000   0.000000   0.000000
yz    0.000000    0.000000    0.000000  40.818194   0.000000   0.000000
xz    0.000000    0.000000    0.000000   0.000000  40.818195   0.000000
xy    0.000000    0.000000    0.000000   0.000000   0.000000  62.761895


====================== piezoelectric tensors available ======================
[PIEZO_RELAXED]
relaxed-ion piezoelectric tensor in Voigt notation (shape: (3, 6))
Units: c/m^2, set to zero below: 1e-05, fit_to_structure: True

          xx        yy        zz        yz        xz   xy
Px  0.000000  0.000000  0.000000  0.000000 -0.048288  0.0
Py  0.000000  0.000000  0.000000 -0.048288  0.000000  0.0
Pz -0.011872 -0.011872  0.064628  0.000000  0.000000  0.0

[PIEZO_CLAMPED]
clamped-ion piezoelectric tensor in Voigt notation (shape: (3, 6))
Units: c/m^2, set to zero below: 1e-05, fit_to_structure: True

          xx        yy       zz        yz        xz   xy
Px  0.000000  0.000000  0.00000  0.000000  0.435488  0.0
Py  0.000000  0.000000  0.00000  0.435488  0.000000  0.0
Pz  0.384901  0.384901 -0.73943  0.000000  0.000000  0.0

Since the DDB file contains internal strain terms and piezoelectric terms, AbiPy set elaflag to 3, instrflag to 1 and piezoflag to 3 so that anaddb will compute both relaxed and clamped-ion tensors.

abilab.docvar("elaflag", executable="anaddb")

Default value:

0

Description

Flag for calculation of elastic and compliance tensors * 0 --> No elastic or compliance tensor will be calculated. * 1 --> Only clamped-ion elastic and compliance tensors will be calculated. Requirements for preceding response-function DDB generation run: Strain perturbation. Set rfstrs to 1, 2, or 3. Note that rfstrs=3 is recommended so that responses to both uniaxial and shear strains will be computed. * 2 --> Both relaxed- and clamped-ion elastic and compliance tensor will be calculated, but only the relaxed-ion quantities will be printed. The input variable anaddb:instrflag should also be set to 1, because the internal-strain tensor is needed to compute the relaxed-ion corrections. Requirements for preceding response-function DDB generation run: Strain and atomic-displacement responses at Q=0. Set rfstrs = 1, 2, or 3 (preferably 3). Set rfatpol and rfdir to do a full calculation of phonons at Q=0 (needed because the inverse of force-constant tensor is required). * 3 --> Both relaxed and clamped-ion elastic and compliance tensors will be printed out. The input variable anaddb:instrflag should also be set to 1. Requirements for preceding response-function DDB generation run: Same as for **elaflag** =2. * 4 --> Calculate the elastic and compliance tensors (relaxed ion) at fixed displacement field, the relaxed-ion tensors at fixed electric field will be printed out too, for comparison. When **elaflag** =4, we need the information of internal strain and relaxed-ion dielectric tensor to build the whole tensor, so we need set anaddb:instrflag=1 and anaddb:dieflag=3 or 4 . * 5 --> Calculate the relaxed ion elastic and compliance tensors, considering the stress left inside cell. At the same time, bare relaxed ion tensors will still be printed out for comparison. In this calculation, stress tensor is needed to compute the correction term, so one is supposed to merge the first order derivative data base (DDB file) with the second order derivative data base (DDB file) into a new DDB file, which can contain both information. And the program will also check for the users.

The tensors are available as attributes of the edata object:

edata.elastic_relaxed

	xx	yy	zz	yz	xz	xy
Voigt index
xx	135.262182	54.450376	38.052927	0.00000	0.000000	0.000000
yy	54.450376	135.262181	38.052927	0.00000	0.000000	0.000000
zz	38.052927	38.052926	148.211029	0.00000	0.000000	0.000000
yz	0.000000	0.000000	0.000000	30.55071	0.000000	0.000000
xz	0.000000	0.000000	0.000000	0.00000	30.550709	0.000000
xy	0.000000	0.000000	0.000000	0.00000	0.000000	40.405903

These are pymatgen tensors, more specifically ElasticTensor objects so we have access to several useful methods. To get the Voigt bulk modulus, use:

edata.elastic_relaxed.k_voigt

75.5386499927217

while the compliance tensor is easily obtained with:

edata.elastic_relaxed.compliance_tensor

ComplianceTensor([[[[ 9.12540966e-03 -6.63185579e-11 -1.35430962e-11]
   [-6.63185579e-11 -3.24901993e-03  5.18499125e-13]
   [-1.35430962e-11  5.18499125e-13 -1.50875299e-03]]

  [[-4.85950967e-11  6.18721480e-03  2.11517754e-13]
   [ 6.18721480e-03  7.09227024e-11 -9.82817856e-13]
   [ 2.11517754e-13 -9.82817856e-13 -1.46075699e-12]]

  [[-1.49197674e-11  2.11523732e-13  8.18311620e-03]
   [ 2.11523732e-13  8.81357700e-12  2.09477889e-12]
   [ 8.18311620e-03  2.09477889e-12  4.38686654e-12]]]


 [[[-4.85950967e-11  6.18721480e-03  2.11517754e-13]
   [ 6.18721480e-03  7.09227024e-11 -9.82817856e-13]
   [ 2.11517754e-13 -9.82817856e-13 -1.46075699e-12]]

  [[-3.24901988e-03  9.91846910e-11  7.06872960e-12]
   [ 9.91846910e-11  9.12540970e-03 -7.17334705e-13]
   [ 7.06872960e-12 -7.17334705e-13 -1.50875296e-03]]

  [[-1.03685440e-13 -1.01063771e-12  2.09477411e-12]
   [-1.01063771e-12 -7.20728753e-13  8.18311576e-03]
   [ 2.09477411e-12  8.18311576e-03 -2.67440577e-13]]]


 [[[-1.49197674e-11  2.11523732e-13  8.18311620e-03]
   [ 2.11523732e-13  8.81357700e-12  2.09477889e-12]
   [ 8.18311620e-03  2.09477889e-12  4.38686654e-12]]

  [[-1.03685440e-13 -1.01063771e-12  2.09477411e-12]
   [-1.01063771e-12 -7.20728753e-13  8.18311576e-03]
   [ 2.09477411e-12  8.18311576e-03 -2.67440577e-13]]

  [[-1.50875300e-03 -3.19970345e-11  4.99090402e-12]
   [-3.19970345e-11 -1.50875290e-03  1.92949068e-13]
   [ 4.99090402e-12  1.92949068e-13  7.52187567e-03]]]])

One can also use the elate online tool to analyse the elastic tensor.

To build a pandas DataFrame with properties derived from the elastic tensor and the associated structure, use:

edata.get_elastic_properties_dataframe(properties_as_index=True)

	property	0	1
0	trans_v	3.194459e+03	3.838052e+03
1	long_v	5.796035e+03	6.295200e+03
2	snyder_ac	5.767044e+01	8.693459e+01
3	snyder_opt	3.158141e-01	3.621134e-01
4	snyder_total	5.798626e+01	8.729670e+01
5	clarke_thermalcond	7.734051e-01	9.006348e-01
6	cahill_thermalcond	8.539415e-01	9.791319e-01
7	debye_temperature	3.760623e+02	4.477874e+02
8	k_voigt	7.553865e+01	7.553930e+01
9	k_reuss	7.553074e+01	7.553579e+01
10	k_vrh	7.553469e+01	7.553754e+01
11	g_voigt	3.951341e+01	5.767416e+01
12	g_reuss	3.761300e+01	5.366047e+01
13	g_vrh	3.856321e+01	5.566731e+01
14	universal_anisotropy	2.527308e-01	3.740360e-01
15	homogeneous_poisson	2.818554e-01	2.041909e-01
16	y_mod	9.886491e+10	1.340681e+11

For the meaning of the different quantities please consult the pymatgen module.

To construct a dataframe with the Voigt indices and the tensor elements use:

edata.get_elastic_voigt_dataframe(tol=1e-5)

	voigt_cinds	elastic_relaxed	elastic_clamped
0	(0, 0)	135.262182	165.988592
1	(0, 1)	54.450376	40.464803
2	(0, 2)	38.052927	21.090298
3	(0, 3)	0.000000	0.000000
4	(0, 4)	0.000000	0.000000
5	(0, 5)	0.000000	0.000000
6	(1, 0)	54.450376	40.464802
7	(1, 1)	135.262181	165.988592
8	(1, 2)	38.052927	21.090299
9	(1, 3)	0.000000	0.000000
10	(1, 4)	0.000000	0.000000
11	(1, 5)	0.000000	0.000000
12	(2, 0)	38.052927	21.090298
13	(2, 1)	38.052926	21.090298
14	(2, 2)	148.211029	182.585743
15	(2, 3)	0.000000	0.000000
16	(2, 4)	0.000000	0.000000
17	(2, 5)	0.000000	0.000000
18	(3, 0)	0.000000	0.000000
19	(3, 1)	0.000000	0.000000
20	(3, 2)	0.000000	0.000000
21	(3, 3)	30.550710	40.818194
22	(3, 4)	0.000000	0.000000
23	(3, 5)	0.000000	0.000000
24	(4, 0)	0.000000	0.000000
25	(4, 1)	0.000000	0.000000
26	(4, 2)	0.000000	0.000000
27	(4, 3)	0.000000	0.000000
28	(4, 4)	30.550709	40.818195
29	(4, 5)	0.000000	0.000000
30	(5, 0)	0.000000	0.000000
31	(5, 1)	0.000000	0.000000
32	(5, 2)	0.000000	0.000000
33	(5, 3)	0.000000	0.000000
34	(5, 4)	0.000000	0.000000
35	(5, 5)	40.405903	62.761895

Note that the Voigt indices are given following the Python © notation in which we start to count from zero.

This might be a bit confusing, especially when comparing with results reported in the literature. The reason why we opted with the 0-based notation is that it facilitates the integration between the DataFrame and other python methods. A similar approach is used in AbiPy when e.g. one has to specify the band or the phonon mode index.

At this point, it should be clear how to analyze the relaxed-ion piezoelectric tensor:

edata.piezo_relaxed

	xx	yy	zz	yz	xz	xy
Voigt index
Px	0.000000	0.000000	0.000000	0.000000	-0.048288	0.0
Py	0.000000	0.000000	0.000000	-0.048288	0.000000	0.0
Pz	-0.011872	-0.011872	0.064628	0.000000	0.000000	0.0

edata.get_piezo_voigt_dataframe(tol=1e-6)

	voigt_cinds	piezo_relaxed	piezo_clamped
0	(0, 0)	0.000000	0.000000
1	(0, 1)	0.000000	0.000000
2	(0, 2)	0.000000	0.000000
3	(0, 3)	0.000000	0.000000
4	(0, 4)	-0.048288	0.435488
5	(0, 5)	0.000000	0.000000
6	(1, 0)	0.000000	0.000000
7	(1, 1)	0.000000	0.000000
8	(1, 2)	0.000000	0.000000
9	(1, 3)	-0.048288	0.435488
10	(1, 4)	0.000000	0.000000
11	(1, 5)	0.000000	0.000000
12	(2, 0)	-0.011872	0.384901
13	(2, 1)	-0.011872	0.384901
14	(2, 2)	0.064628	-0.739430
15	(2, 3)	0.000000	0.000000
16	(2, 4)	0.000000	0.000000
17	(2, 5)	0.000000	0.000000

Convergence study wrt the number of k-points#

In this part of the tutorial, we discuss how to compute elastic and piezoelectric tensors with different k-point meshes and how to use the DdbRobot to analyze the results.

In principle, one should relax the structure with different k-point samplings and then use the relaxed structure to compute elastic and piezoelectric properties. This is easy with AbiPy but, for the time being, we ignore this point and use the same structure so that we can learn how to use Python to analyze multiple calculations. At the end of this tutorial you will find an example of flow in which the structural relaxation is performed with different k-meshes.

Since we do not have to change the structure, performing a convergence study with respect to k-points is just a matter of creating multiple Works inside a loop over k-meshes (our make_scf_input is already accepting ngkpt in input):

from lesson_elastic import build_ngkpt_convflow
abilab.print_source(build_ngkpt_convflow)

def build_ngkpt_convflow(options=None, ngkpt_list=([2, 2, 2], [4, 4, 4], [8, 8, 8])):
    """
    Build and return a flow computing elastic and piezoelectric properties with
    different k-point samplings given in `ngkpt_list`.
    In principle, one should perform different structural relaxations for each `ngkpt`
    and use the relaxed structures to compute elastic properties.
    """
    workdir = options.workdir if (options and options.workdir) else "flow_elastic_ngkpt_conv"

    flow = flowtk.Flow(workdir=workdir)

    for ngkpt in ngkpt_list:
        scf_input = make_scf_input(ngkpt=ngkpt)

        elast_work = flowtk.ElasticWork.from_scf_input(scf_input, with_relaxed_ion=True, with_piezo=True)

        flow.register_work(elast_work)

    return flow

ngkpt_flow = build_ngkpt_convflow(options=None, ngkpt_list=([2, 2, 2], [4, 4, 4], [8, 8, 8]))

ngkpt_flow.get_graphviz()

../_images/d1b0b478f4b36d5724715dba292bc52598569489bf5507d6ec68c2ee8407cc29.svg

#ngkpt_flow.get_vars_dataframe("ngkpt")

To generate the flow with the lesson_elastic.py script, open the file, comment the call to build_flow and uncomment build_ngkpt_convflow. Then run the script and launch the calculation with:

abirun.py flow_elastic_ngkpt_conv scheduler

as usual.

There are several output files located inside the outdata directories:

!find flow_elastic_ngkpt_conv/ -name "*_DDB"

flow_elastic_ngkpt_conv/w2/outdata/out_DDB
flow_elastic_ngkpt_conv/w1/outdata/out_DDB
flow_elastic_ngkpt_conv/w0/outdata/out_DDB

Remember that our goal is to analyze the convergence of the elastic and piezoelectric properties as function of nkpt. So we are mainly interested in the final DDB files located in the outdata directories of the works (w0/outdata, w1/outdata, w2/outdata). These are indeed the DDB files with all the information needed in anaddb to compute the tensors.

The code below tells our robot that we would like to analyze all the DDB files located in the output directories of the works:

robot = abilab.DdbRobot.from_dir_glob("./flow_elastic_ngkpt_conv/w*/outdata/")
robot

flow_elastic_ngkpt_conv/w2/outdata/out_DDB
flow_elastic_ngkpt_conv/w1/outdata/out_DDB
flow_elastic_ngkpt_conv/w0/outdata/out_DDB

The DDB file are available in robot.abifile. Each DdbFile object has a header (dictionary) containing metadata extracted from the DDB file. To get the keywords in the header, use:

robot.abifiles[0].header.keys()

dict_keys(['version', 'lines', 'usepaw', 'natom', 'nkpt', 'nsppol', 'nsym', 'ntypat', 'occopt', 'nband', 'acell', 'amu', 'dilatmx', 'ecut', 'ecutsm', 'intxc', 'iscf', 'ixc', 'kpt', 'kptnrm', 'ngfft', 'nspden', 'nspinor', 'occ', 'rprim', 'dfpt_sciss', 'spinat', 'symafm', 'symrel', 'tnons', 'tolwfr', 'tphysel', 'tsmear', 'typat', 'wtk', 'xred', 'znucl', 'zion'])

We will be using these meta variables to construct our pandas Dataframe so that we can analyze the convergence of our physical quantities with e.g. nkpt.

Let’s call anacompare_elastic to construct a DataFrame (data) with the elastic properties obtained with the three DDB files and add the value of ddb.header["nkpt"]. elastdata_list is a list of ElastData object we can use afterwards to access the individual tensors:

data, elastdata_list = robot.anacompare_elastic(ddb_header_keys="nkpt")

data.keys()

Index(['trans_v', 'long_v', 'snyder_ac', 'snyder_opt', 'snyder_total',
       'clarke_thermalcond', 'cahill_thermalcond', 'debye_temperature',
       'k_voigt', 'k_reuss', 'k_vrh', 'g_voigt', 'g_reuss', 'g_vrh',
       'universal_anisotropy', 'homogeneous_poisson', 'y_mod', 'tensor_name',
       'formula', 'nkpt', 'natom', 'alpha', 'beta', 'gamma', 'a', 'b', 'c',
       'volume', 'abispg_num', 'spglib_symb', 'spglib_num',
       'spglib_lattice_type'],
      dtype='object')

data

	trans_v	long_v	snyder_ac	snyder_opt	snyder_total	clarke_thermalcond	cahill_thermalcond	debye_temperature	k_voigt	k_reuss	...	beta	gamma	a	b	c	volume	spglib_symb	spglib_num	spglib_lattice_type
0	3187.357490	5761.696015	56.983956	0.314556	57.298512	0.770980	0.850540	375.118016	74.267964	74.258479	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal
1	3849.753468	6277.945639	87.049415	0.362273	87.411688	0.901308	0.979563	448.886026	74.268035	74.260840	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal
2	3194.458696	5796.034979	57.670442	0.315814	57.986256	0.773405	0.853941	376.062257	75.538650	75.530735	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal
3	3838.051896	6295.200076	86.934586	0.362113	87.296699	0.900635	0.979132	447.787424	75.539303	75.535785	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal
4	3151.515933	5705.015874	55.194905	0.311229	55.506134	0.762578	0.841544	370.940943	73.572019	72.331727	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal
5	3753.376690	6179.896893	81.728454	0.354736	82.083190	0.882070	0.959183	438.077881	73.667176	73.014097	...	90.0	120.0	3.989448	3.989448	6.49713	89.552529	P6_3mc	186	hexagonal

6 rows × 32 columns

data[["k_voigt", "nkpt", "tensor_name"]]

	k_voigt	nkpt	tensor_name
0	74.267964	40	elastic_relaxed
1	74.268035	40	elastic_clamped
2	75.538650	8	elastic_relaxed
3	75.539303	8	elastic_clamped
4	73.572019	2	elastic_relaxed
5	73.667176	2	elastic_clamped

To plot the convergence of selected properties versus the number of k-points, use:

robot.plot_xy_with_hue(data, x="nkpt", y=["k_voigt", "g_voigt", "y_mod"], hue="tensor_name");

../_images/5582be43def70eef97c4a3af5dd925654d18d5e1c73ee3f8356a395bb7878591.png

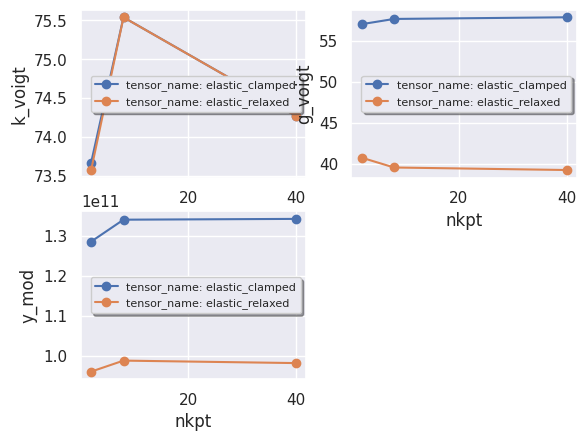
For more examples on the use of DDB and robots, see the DDB notebook

Now let’s try something a bit more complicated. Assume we want to plot the convergence of the individual elements of the tensor as as function of nkpt. In this case, we have to work a bit more to create a Dataframe with the elements in Voigt notation, add the value of nkpt associated to this tensor and finally concatenate the results in a single DataFrame:

df_list = []
for edata, ddb in zip(elastdata_list, robot.abifiles):

    # Get dataframe with tensor elements in Voigt notation
    df = edata.get_elastic_voigt_dataframe()

    # Add metadata and store dataframe in df_list
    df["nkpt"] = ddb.header["nkpt"]
    df_list.append(df)

# Concatenate dataframes
import pandas as pd
data = pd.concat(df_list)
data.head()

	voigt_cinds	elastic_relaxed	elastic_clamped	nkpt
0	(0, 0)	1.309889e+02	1.628166e+02	40
1	(0, 1)	5.249070e+01	3.820562e+01	40
2	(0, 2)	3.807428e+01	2.045653e+01	40
3	(0, 3)	4.710262e-09	4.611456e-09	40
4	(0, 4)	7.390751e-08	-5.268783e-09	40

To select only the (0, 0) elements, use the syntax:

c00 = data[data["voigt_cinds"] == (0, 0)]
c00

voigt_cinds	elastic_relaxed	elastic_clamped	nkpt
(0, 0)	130.988919	162.816606	40
(0, 0)	135.262182	165.988592	8
(0, 0)	152.688699	177.895515	2

Now we can finally plot the (0, 0) tensor elements as function of nkpt with:

c00.plot(x="nkpt", y=[k for k in c00 if k.startswith("elastic_")], subplots=True, style="-o");

../_images/5f9c11e175ab5aa171a0e90be1b9fb40b5a899efc4bbede0b7c2c05cce61183c.png

Elastic and piezoelectric properties with Abinit and AbiPy

Contents

Elastic and piezoelectric properties with Abinit and AbiPy#

DFPT calculation of elastic and piezolectric tensors#

Default value:

Description

Post-processing the results#

Default value:

Description

Convergence study wrt the number of k-points#