The GSR file (Ground-State Results)#
In this notebook, we discuss how to plot electronic band structures and densities of states (DOS) using the GSR netcdf files produced by Abinit.
In this tutorial, we use the netcdf files shipped with AbiPy.
The function abidata.ref_file returns the absolute path of a reference file.
In your scripts, you should replace abidata.ref_file("abipy_filename") with a string giving
the location of your netcdf file.
Alternatively, you can use the abiopen.py script to open the file from the shell with:
abiopen.py out_GSR.nc
This command starts the IPython interpreter so that you can interact directly
with the GsrFile object (named abifile inside IPython).
To generate a Jupyter notebook, use:
abiopen.py out_GSR.nc -nb
For a quick visualization of the data, use the --expose option:
abiopen.py out_GSR.nc -e
Note
Simple visualization tasks can be easily automated by just issuing in the terminal:
abiopen.py FILE --expose
to generate a predefined list of matplotlib plots.
To activate the plotly version (if available) use:
abiopen.py FILE --plotly
Note also that one can generate jupyter-lab notebooks directly from the command line with abiopen.py and the command:
abiopen.py FILE -nb
Add --classic-notebook if you prefer classic jupyter notebooks.
Finally, use one of the options of the abiview.py script to plot the results automatically.
import warnings
warnings.filterwarnings("ignore") # Ignore warnings
from abipy import abilab
abilab.enable_notebook() # This line tells AbiPy we are running inside a notebook
# Import abipy reference data.
import abipy.data as abidata
# This line configures matplotlib to show figures embedded in the notebook.
# Replace `inline` with `notebook` in classic notebook
%matplotlib inline
# Option available in jupyterlab. See https://github.com/matplotlib/jupyter-matplotlib
#%matplotlib widget
The GSR File#
The GSR file (mnemonic: Ground-State Results) is a netcdf file with the
results produced by SCF or NSCF ground-state calculations
(band energies, forces, total energy, stress tensor).
To open a GSR file, use the abiopen function defined in abilab:
gsr = abilab.abiopen(abidata.ref_file("si_scf_GSR.nc"))
The gsr object has a Structure:
print(gsr.structure)
Full Formula (Si2)
Reduced Formula: Si
abc : 3.866975 3.866975 3.866975
angles: 60.000000 60.000000 60.000000
pbc : True True True
Sites (2)
# SP a b c cartesian_forces
--- ---- ---- ---- ---- -----------------------------------------------------------
0 Si 0 0 0 [-5.89948307e-27 -1.93366149e-27 2.91016904e-27] eV ang^-1
1 Si 0.25 0.25 0.25 [ 5.89948307e-27 1.93366149e-27 -2.91016904e-27] eV ang^-1
min |F_iat|: 6.856532001208972e-27 eV/Ang
max |F_iat|: 6.856532001208972e-27 eV/Ang
mean F_iat|: 6.856532001208972e-27 eV/Ang
std |F_iat|: 0.0 eV/Ang
Forces are relaxed within high quality criterion: 0.0001 eV/Ang
Abinit Spacegroup: spgid: 227, num_spatial_symmetries: 48, has_timerev: True, symmorphic: True
and an ElectronBands object with the band energies, the occupation factors and the list of \(k\)-points:
print(gsr.ebands)
================================= Structure =================================
Full Formula (Si2)
Reduced Formula: Si
abc : 3.866975 3.866975 3.866975
angles: 60.000000 60.000000 60.000000
pbc : True True True
Sites (2)
# SP a b c cartesian_forces
--- ---- ---- ---- ---- -----------------------------------------------------------
0 Si 0 0 0 [-5.89948307e-27 -1.93366149e-27 2.91016904e-27] eV ang^-1
1 Si 0.25 0.25 0.25 [ 5.89948307e-27 1.93366149e-27 -2.91016904e-27] eV ang^-1
min |F_iat|: 6.856532001208972e-27 eV/Ang
max |F_iat|: 6.856532001208972e-27 eV/Ang
mean F_iat|: 6.856532001208972e-27 eV/Ang
std |F_iat|: 0.0 eV/Ang
Forces are relaxed within high quality criterion: 0.0001 eV/Ang
Abinit Spacegroup: spgid: 227, num_spatial_symmetries: 48, has_timerev: True, symmorphic: True
Number of electrons: 8.0, Fermi level: 5.598 (eV)
nsppol: 1, nkpt: 29, mband: 8, nspinor: 1, nspden: 1
smearing scheme: none (occopt 1), tsmear_eV: 0.272, tsmear Kelvin: 3157.7
Direct gap:
Energy: 2.532 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Final state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 4, eig: 8.130, occ: 0.000
Fundamental gap:
Energy: 0.562 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Final state: spin: 0, kpt: [+0.375, +0.375, +0.000], weight: 0.012, band: 4, eig: 6.161, occ: 0.000
Bandwidth: 11.856 (eV)
Valence maximum located at kpt index 0:
spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Conduction minimum located at kpt index 17:
spin: 0, kpt: [+0.375, +0.375, +0.000], weight: 0.012, band: 4, eig: 6.161, occ: 0.000
TIP: Use `--verbose` to print k-point coordinates with more digits
Important
Python counts from zero, thus the first band has index 0 and the first spin is 0. AbiPy uses the same convention, so be very careful when specifying band, spin or \(k\)-point indices.
A GSR file produced by a self-consistent run contains the values of the total energy, the forces, and the stress tensor at the end of the SCF cycle:
print("energy:", gsr.energy, "pressure:", gsr.pressure)
energy: -241.23647031321218 eV pressure: -5.211617575719521 GPa
To get a summary of the most important results:
print(gsr)
================================= File Info =================================
Name: si_scf_GSR.nc
Directory: /home/runner/work/abipy_book/abipy_book/abipy/abipy/data/refs/si_ebands
Size: 14.83 kB
Access Time: Wed Sep 30 15:59:07 2026
Modification Time: Wed Sep 30 15:58:18 2026
Change Time: Wed Sep 30 15:58:18 2026
================================= Structure =================================
Full Formula (Si2)
Reduced Formula: Si
abc : 3.866975 3.866975 3.866975
angles: 60.000000 60.000000 60.000000
pbc : True True True
Sites (2)
# SP a b c cartesian_forces
--- ---- ---- ---- ---- -----------------------------------------------------------
0 Si 0 0 0 [-5.89948307e-27 -1.93366149e-27 2.91016904e-27] eV ang^-1
1 Si 0.25 0.25 0.25 [ 5.89948307e-27 1.93366149e-27 -2.91016904e-27] eV ang^-1
min |F_iat|: 6.856532001208972e-27 eV/Ang
max |F_iat|: 6.856532001208972e-27 eV/Ang
mean F_iat|: 6.856532001208972e-27 eV/Ang
std |F_iat|: 0.0 eV/Ang
Forces are relaxed within high quality criterion: 0.0001 eV/Ang
Abinit Spacegroup: spgid: 227, num_spatial_symmetries: 48, has_timerev: True, symmorphic: True
Stress tensor (Cartesian coordinates in GPa):
[[5.21161758e+00 7.86452261e-11 0.00000000e+00]
[7.86452261e-11 5.21161758e+00 0.00000000e+00]
[0.00000000e+00 0.00000000e+00 5.21161758e+00]]
Pressure: -5.212 (GPa)
Energy: -241.23647031 (eV)
============================== Electronic Bands ==============================
Number of electrons: 8.0, Fermi level: 5.598 (eV)
nsppol: 1, nkpt: 29, mband: 8, nspinor: 1, nspden: 1
smearing scheme: none (occopt 1), tsmear_eV: 0.272, tsmear Kelvin: 3157.7
Direct gap:
Energy: 2.532 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Final state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 4, eig: 8.130, occ: 0.000
Fundamental gap:
Energy: 0.562 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Final state: spin: 0, kpt: [+0.375, +0.375, +0.000], weight: 0.012, band: 4, eig: 6.161, occ: 0.000
Bandwidth: 11.856 (eV)
Valence maximum located at kpt index 0:
spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.002, band: 3, eig: 5.598, occ: 2.000
Conduction minimum located at kpt index 17:
spin: 0, kpt: [+0.375, +0.375, +0.000], weight: 0.012, band: 4, eig: 6.161, occ: 0.000
TIP: Use `--verbose` to print k-point coordinates with more digits
The different contributions to the total energy are stored in a dictionary:
print(gsr.energy_terms)
Term Value
e_localpsp -68.62575673513619 eV
e_eigenvalues 4.453251818688362 eV
e_ewald -226.94266726062642 eV
e_hartree 14.989583992483517 eV
e_corepsp 2.2624802653426976 eV
e_corepspdc 0.0 eV
e_kinetic 80.66035184380631 eV
e_nonlocalpsp 52.15353088289424 eV
e_entropy 0.0 eV
entropy 0.0 eV
e_xc -95.73399330197637 eV
e_xcdc 0.0 eV
e_paw 0.0 eV
e_pawdc 0.0 eV
e_elecfield 0.0 eV
e_magfield 0.0 eV
e_fermie 5.598453325101502 eV
e_sicdc 0.0 eV
e_exactX 0.0 eV
h0 0.0 eV
e_electronpositron 0.0 eV
edc_electronpositron 0.0 eV
e0_electronpositron 0.0 eV
e_monopole 0.0 eV
At this point, we don’t need this file anymore, so we close it with:
gsr.close()
Warning
The gsr object keeps a reference to the underlying netcdf file, hence one should
call gsr.close() to release the resource when the file is no longer needed.
Python does this automatically if you use abiopen with the with context manager.
Note that we don’t always follow this rule inside Jupyter notebooks, to keep the code readable, but you should definitely close all your files, especially when writing code that may run for hours or even longer.
Plotting band structures#
Let’s open the GSR file produced by an NSCF calculation on a high-symmetry \(k\)-path and extract the electronic band structure.
Pymatgen issues a warning about the structure not being standard. Be aware that this might affect the automatic labelling of the boundary \(k\)-points on the path, so carefully check the \(k\)-point labels in the figures produced in such cases. In the present case, the labelling is correct.
with abilab.abiopen(abidata.ref_file("si_nscf_GSR.nc")) as nscf_gsr:
ebands_kpath = nscf_gsr.ebands
Now we can plot the band energies with matplotlib:
# The labels for the k-points are found in an internal database.
ebands_kpath.plot(with_gaps=True, title="Silicon band structure");
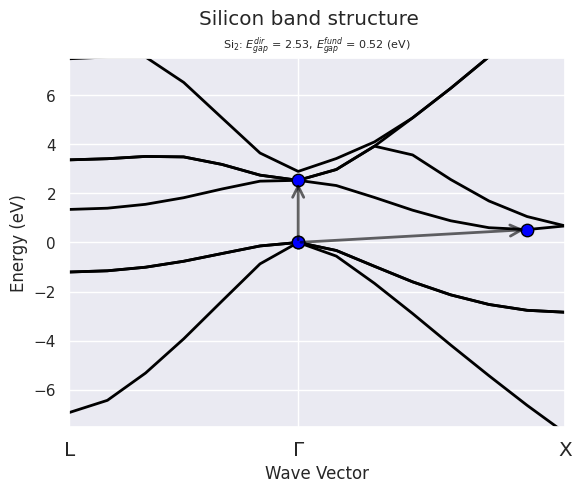
Alternatively, one can use the optional argument klabels to define the mapping
reduced_coordinates --> name of the k-point and pass it to the plot method:
klabels = {
(0.5, 0.0, 0.0): "L",
(0.0, 0.0, 0.0): "$\Gamma$",
(0.0, 0.5, 0.5): "X"
}
# ebands_kpath.plot(title="User-defined k-labels", band_range=(0, 5), klabels=klabels);
For the plotly version, use:
ebands_kpath.plotly(with_gaps=True, title="Silicon band structure with plotly");
To build a panel GUI exposing the methods of the GSR file, use:
abilab.abipanel()
gsr.get_panel()
This cell is not executed in the online book, since the GUI requires a live Jupyter notebook.
Let’s have a look at our \(k\)-points by calling kpoints.plotly()
ebands_kpath.kpoints.plotly();
and the crystalline structure with:
ebands_kpath.structure.plot();
Note
The same piece of code works if you replace the GSR.nc file with e.g. a WFK.nc file
(actually, with any netcdf file containing an ebands object).
The main advantage of the GSR file is that it is lightweight (no wavefunctions).
DOS with the Gaussian technique#
Let’s use the eigenvalues and the \(k\)-point weights stored in ebands_kmesh to
compute the DOS with the Gaussian method.
The method is called without arguments, so default values are used
for the broadening and the step of the linear mesh.
with abilab.abiopen(abidata.ref_file("si_scf_GSR.nc")) as scf_gsr:
ebands_kmesh = scf_gsr.ebands
edos = ebands_kmesh.get_edos()
print(edos)
nsppol: 1, nelect: 8.0
Fermi energy: 5.868068972680834 (eV) (recomputed from nelect):
edos.plotly();
print("[ebands_kmesh] is_ibz:", ebands_kmesh.kpoints.is_ibz, "is_kpath:", ebands_kmesh.kpoints.is_path)
print("[ebands_kpath] is_ibz:", ebands_kpath.kpoints.is_ibz, "is_kpath:", ebands_kpath.kpoints.is_path)
[ebands_kmesh] is_ibz: True is_kpath: False
[ebands_kpath] is_ibz: False is_kpath: True
Warning
The DOS requires a homogeneous \(k\)-sampling of the BZ. AbiPy raises an exception if you try to compute the DOS with a \(k\)-path.
To plot bands and DOS on the same figure:
ebands_kpath.plotly_with_edos(edos, with_gaps=True);
To plot the DOS and the integrated DOS (IDOS), use:
edos.plotly_dos_idos();
The Gaussian broadening can significantly change the overall shape of the DOS. If accurate values are needed (e.g. the DOS at the Fermi level in metals), one should perform a careful convergence study with respect to the \(k\)-point mesh. Here we show how to compute the DOS with different values of the Gaussian smearing for a fixed \(k\)-point sampling, and how to plot the results:
# Compute the DOS with the Gaussian method and different values of the broadening
widths = [0.1, 0.2, 0.3, 0.4]
edos_plotter = ebands_kmesh.compare_gauss_edos(widths, step=0.1)
To plot the results on the same figure, use:
edos_plotter.combiplot(title="e-DOS as function of the Gaussian broadening");
while gridplot generates a grid of subplots:
edos_plotter.gridplot();
Joint density of states#
This example shows how to plot the different contributions to the electronic joint density of states (JDOS) of silicon. First, we select the valence and conduction bands to be included in the JDOS. Here we include the valence bands from 0 to 3 and the first conduction band (4).
vrange = range(0,4)
crange = range(4,5)
# Plot data
ebands_kmesh.plot_ejdosvc(vrange, crange);
ebands_kpath.plot_transitions(omega_ev=3.0);
ebands_kmesh.plot_transitions(omega_ev=3.0);
Plotting the Fermi surface#
with abilab.abiopen(abidata.ref_file("mgb2_kmesh181818_FATBANDS.nc")) as fbnc_kmesh:
mgb2_ebands = fbnc_kmesh.ebands
# Build ebands in full BZ.
mgb2_eb3d = mgb2_ebands.get_ebands3d()
In MgB\(_2\), three bands cross the Fermi level (bands 2, 3 and 4):
mgb2_ebands.boxplot();
Let’s use matplotlib to plot the isosurfaces at the Fermi level (default):
# Warning: requires skimage package, rendering could be slow.
mgb2_eb3d.plot_isosurfaces();
#ebands_kpath.plot_scatter3d(band=3);
#ebands_kmesh.plot_scatter3d(band=3);
Analyzing multiple GSR files with robots#
TODO
Note
Robots can also be constructed from the command line with abicomp.py gsr FILES.