The SIGRES file (GW)#
This notebook explains how to use AbiPy and matplotlib to visualize the results produced by the GW code.
The self-energy code (optdriver 4) saves the final results in the SIGRES.nc file
while the screening code (optdriver 3) stores the inverse dielectric matrix in the SCR.nc file.
Let’s start by importing the basic modules we will need for this tutorial.
import warnings
warnings.filterwarnings("ignore") # Ignore warnings
from abipy import abilab
abilab.enable_notebook() # This line tells AbiPy we are running inside a notebook
import abipy.data as abidata
# This line configures matplotlib to show figures embedded in the notebook.
# Replace `inline` with `notebook` in classic notebook
%matplotlib inline
# Option available in jupyterlab. See https://github.com/matplotlib/jupyter-matplotlib
#%matplotlib widget
How to visualize QP corrections#
As usual, we start by opening the netcdf file with abiopen:
sigres = abilab.abiopen(abidata.ref_file("tgw1_9o_DS4_SIGRES.nc"))
print(sigres)
================================= File Info =================================
Name: tgw1_9o_DS4_SIGRES.nc
Directory: /home/runner/work/abipy_book/abipy_book/abipy/abipy/data/refs
Size: 1005.34 kB
Access Time: Thu Jan 15 12:20:36 2026
Modification Time: Thu Jan 15 12:15:09 2026
Change Time: Thu Jan 15 12:15:09 2026
================================= Structure =================================
Full Formula (Si2)
Reduced Formula: Si
abc : 3.823046 3.823046 3.823046
angles: 60.000000 60.000000 60.000000
pbc : True True True
Sites (2)
# SP a b c
--- ---- ---- ---- ----
0 Si 0 0 0
1 Si 0.25 0.25 0.25
Abinit Spacegroup: spgid: 0, num_spatial_symmetries: 48, has_timerev: True, symmorphic: True
============================== Kohn-Sham bands ==============================
Number of electrons: 8.0, Fermi level: 5.951 (eV)
nsppol: 1, nkpt: 6, mband: 100, nspinor: 1, nspden: 1
smearing scheme: (occopt 1), tsmear_eV: 1.088, tsmear Kelvin: 12631.0
Direct gap:
Energy: 2.513 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.031, band: 3, eig: 5.951, occ: 2.000
Final state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.031, band: 4, eig: 8.464, occ: 0.000
Fundamental gap:
Energy: 0.570 (eV)
Initial state: spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.031, band: 3, eig: 5.951, occ: 2.000
Final state: spin: 0, kpt: [+0.500, +0.500, +0.000], weight: 0.094, band: 4, eig: 6.521, occ: 0.000
Bandwidth: 12.096 (eV)
Valence maximum located at kpt index 5:
spin: 0, kpt: [+0.000, +0.000, +0.000], weight: 0.031, band: 3, eig: 5.951, occ: 2.000
Conduction minimum located at kpt index 2:
spin: 0, kpt: [+0.500, +0.500, +0.000], weight: 0.094, band: 4, eig: 6.521, occ: 0.000
TIP: Use `--verbose` to print k-point coordinates with more digits
=============================== QP direct gaps ===============================
QP_dirgap: 3.537 (eV) for k-point: [-0.250, -0.250, +0.000], spin: 0
QP_dirgap: 4.357 (eV) for k-point: [-0.250, +0.250, +0.000], spin: 0
QP_dirgap: 4.117 (eV) for k-point: X [+0.500, +0.500, +0.000], spin: 0
QP_dirgap: 8.711 (eV) for k-point: W [-0.250, +0.500, +0.250], spin: 0
QP_dirgap: 3.297 (eV) for k-point: L [+0.500, +0.000, +0.000], spin: 0
QP_dirgap: 3.126 (eV) for k-point: $\Gamma$ [+0.000, +0.000, +0.000], spin: 0
============== QP results for each k-point and spin (all in eV) ==============
K-point: [-0.250, -0.250, +0.000], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme \
0 0 -5.046 -4.760 -4.561 -10.493 -16.549 6.542 1.344e-321
1 1 2.411 2.281 2.238 -11.089 -13.671 2.410 1.344e-321
2 2 4.008 3.867 3.825 -10.689 -12.566 1.694 1.344e-319
3 3 4.008 3.867 3.825 -10.689 -12.566 1.695 1.334e-322
4 4 6.963 7.405 7.523 -9.434 -5.330 -3.544 8.053e-322
5 5 8.979 9.462 9.594 -9.212 -4.504 -4.093 1.636e-152
6 6 11.702 12.132 12.276 -10.569 -5.276 -4.719 1.344e-321
7 7 11.702 12.133 12.278 -10.569 -5.276 -4.717 1.344e-321
ze0
0 0.589
1 0.751
2 0.768
3 0.769
4 0.789
5 0.786
6 0.748
7 0.748
K-point: [-0.250, +0.250, +0.000], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme \
0 0 -4.064 -3.960 -3.904 -10.617 -16.264 5.808 1.340e-319
1 1 0.418 0.303 0.258 -10.811 -14.348 3.376 0.000e+00
2 2 2.088 1.979 1.944 -10.067 -12.427 2.216 0.000e+00
3 3 4.590 4.437 4.391 -10.912 -12.687 1.576 0.000e+00
4 4 8.311 8.793 8.925 -9.604 -5.066 -3.924 5.774e-313
5 5 10.711 11.188 11.335 -10.115 -4.841 -4.649 1.334e-322
6 6 11.052 11.455 11.573 -10.233 -5.401 -4.310 2.668e-322
7 7 11.990 12.395 12.526 -9.894 -4.357 -5.001 0.000e+00
ze0
0 0.652
1 0.723
2 0.758
3 0.770
4 0.786
5 0.764
6 0.773
7 0.756
K-point: X [+0.500, +0.500, +0.000], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme \
0 0 -1.936 -1.940 -1.947 -10.762 -15.448 4.680 1.732e-312
1 1 -1.936 -1.944 -1.942 -10.762 -15.448 4.675 6.719e-322
2 2 3.030 2.851 2.795 -10.568 -12.966 2.163 0.000e+00
3 3 3.030 2.851 2.795 -10.568 -12.966 2.163 5.774e-313
4 4 6.521 6.968 7.084 -9.078 -5.038 -3.478 5.774e-313
5 5 6.521 6.969 7.084 -9.078 -5.038 -3.477 1.334e-322
6 6 15.976 16.184 16.280 -10.528 -3.786 -6.438 0.000e+00
7 7 15.976 16.185 16.282 -10.528 -3.786 -6.437 5.385e-322
ze0
0 0.700
1 0.701
2 0.762
3 0.761
4 0.795
5 0.795
6 0.685
7 0.684
K-point: W [-0.250, +0.500, +0.250], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme \
0 0 -1.760 -1.773 -1.808 -10.873 -15.503 4.611 6.722e-320
1 1 -1.760 -1.793 -1.778 -10.873 -15.503 4.582 1.334e-322
2 2 1.982 1.867 1.830 -9.991 -12.434 2.290 0.000e+00
3 3 1.982 1.867 1.830 -9.991 -12.434 2.290 0.000e+00
4 4 10.159 10.578 10.696 -9.647 -4.967 -4.142 6.722e-320
5 5 10.159 10.577 10.697 -9.647 -4.967 -4.143 0.000e+00
6 6 10.902 11.366 11.509 -10.031 -4.701 -4.722 0.000e+00
7 7 10.902 11.366 11.509 -10.031 -4.701 -4.722 0.000e+00
ze0
0 0.691
1 0.691
2 0.757
3 0.757
4 0.779
5 0.779
6 0.764
7 0.764
K-point: L [+0.500, +0.000, +0.000], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme \
0 0 -3.760 -3.647 -3.578 -10.759 -16.296 5.719 0.000e+00
1 1 -1.137 -1.182 -1.198 -10.178 -14.330 4.091 5.543e-311
2 2 4.726 4.559 4.509 -11.006 -12.812 1.588 0.000e+00
3 3 4.726 4.559 4.509 -11.006 -12.812 1.588 0.000e+00
4 4 7.408 7.856 7.978 -10.054 -5.736 -3.748 0.000e+00
5 5 9.251 9.772 9.915 -9.698 -4.959 -4.074 0.000e+00
6 6 9.251 9.771 9.916 -9.698 -4.959 -4.075 0.000e+00
7 7 13.458 13.754 13.847 -8.011 -2.413 -5.210 0.000e+00
ze0
0 0.623
1 0.737
2 0.772
3 0.772
4 0.785
5 0.783
6 0.783
7 0.760
K-point: $\Gamma$ [+0.000, +0.000, +0.000], spin: 0
band e0 qpe qpe_diago vxcme sigxme sigcmee0 vUme ze0
0 0 -6.145 -5.719 -5.412 -10.388 -16.893 7.239 0.0 0.581
1 1 5.951 5.806 5.764 -11.253 -12.628 1.188 0.0 0.777
2 2 5.951 5.806 5.764 -11.253 -12.628 1.188 0.0 0.777
3 3 5.951 5.806 5.764 -11.253 -12.628 1.187 0.0 0.777
4 4 8.464 8.931 9.065 -10.042 -5.563 -3.878 0.0 0.777
5 5 8.464 8.932 9.066 -10.042 -5.563 -3.877 0.0 0.777
6 6 8.464 8.933 9.067 -10.042 -5.563 -3.876 0.0 0.778
7 7 9.205 9.664 9.798 -10.748 -5.734 -4.421 0.0 0.773
Let’s have a look at the KS energies used to compute the Green’s function \(G_0\), the RPA screening \(W_0\) and the \(G_0W_0\) self-energy:
sigres.ebands.plot();
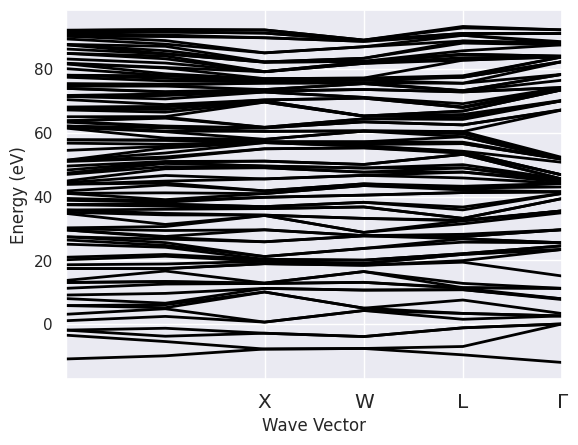
The SIGRES file contains the KS as well as the QP direct gaps for all the k-points included in the calculation (kptgw). To plot the difference QP - KS, use:
sigres.plot_qpgaps();
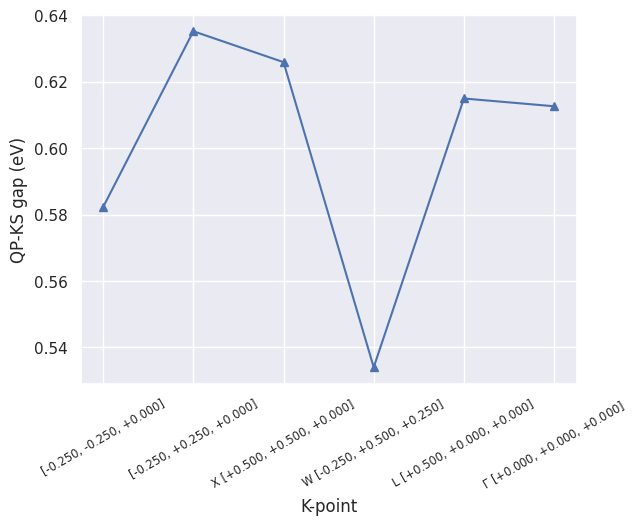
For the absolute QP gaps:
sigres.plot_qpgaps(plot_qpmks=False);
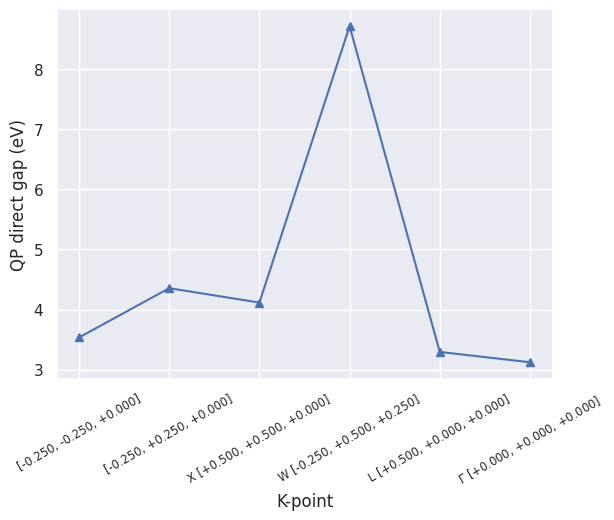
To plot the QP results as a function of the initial KS energy:
sigres.plot_qps_vs_e0(); #tight_layout=True);
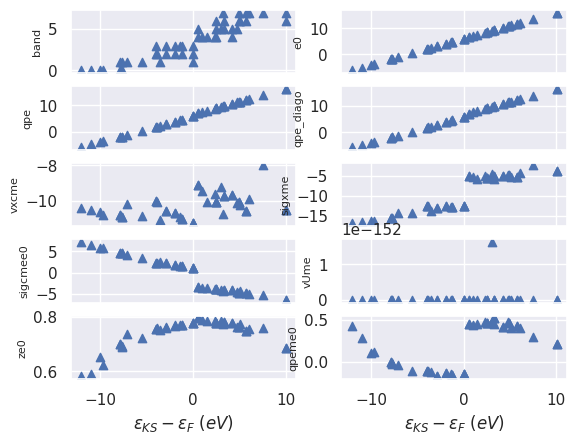
and use with_fields to filter the quantity of interest:
sigres.plot_qps_vs_e0(with_fields=["vxcme", "sigxme", "sigcmee0"], sharey=True);
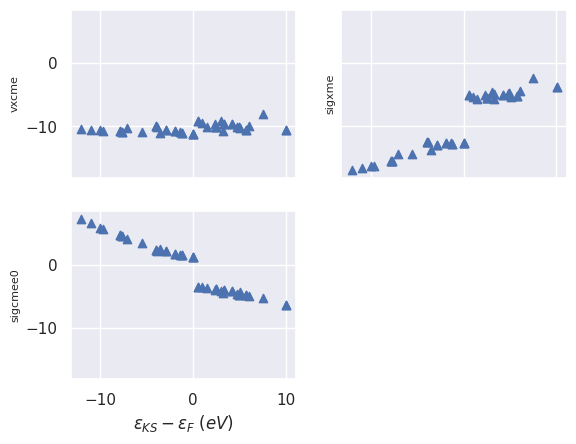
To plot the QP energies on top of the KS energies used in the SIGMA run:
sigres.plot_qpbands_ibz();
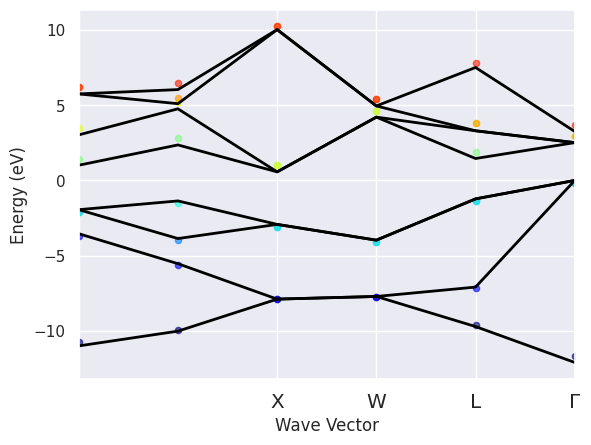
To plot the KS band structure with markers whose size is proportional to the QP correction and whose direction gives the sign of the correction:
sigres.plot_ksbands_with_qpmarkers(fact=1000);
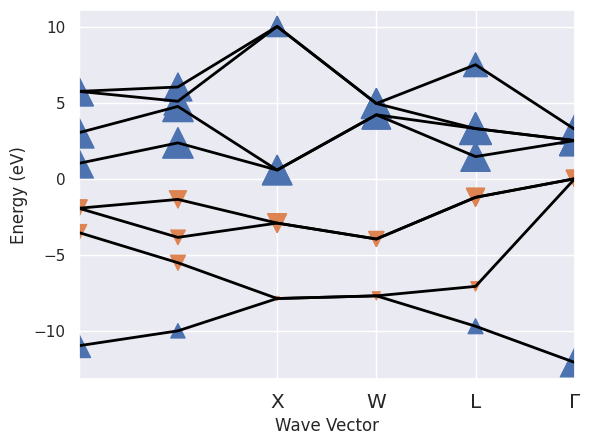
We can also plot the \(<\Psi^{KS}_{mk}\,|\,\Psi^{QP}_{nk}>\) coefficients for given spin and k-point:
sigres.plot_eigvec_qp(spin=0, kpoint=0);
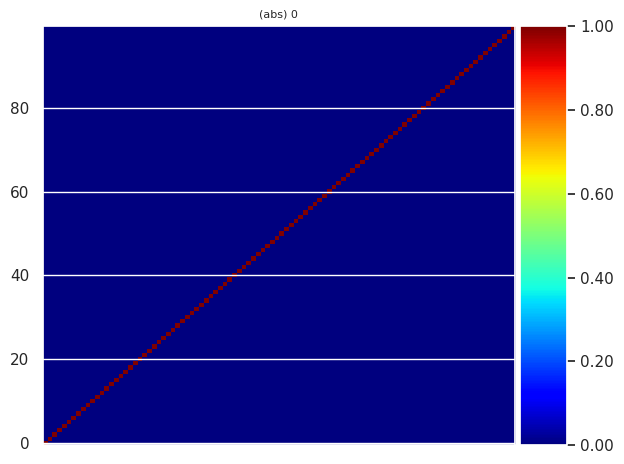
In this case, we have a diagonal matrix because the wavefunctions are not updated (\(G_0W_0\)). The scenario is completely different if you start to perform self-consistent calculations with update of the QP amplitudes.
Plotting the spectral function#
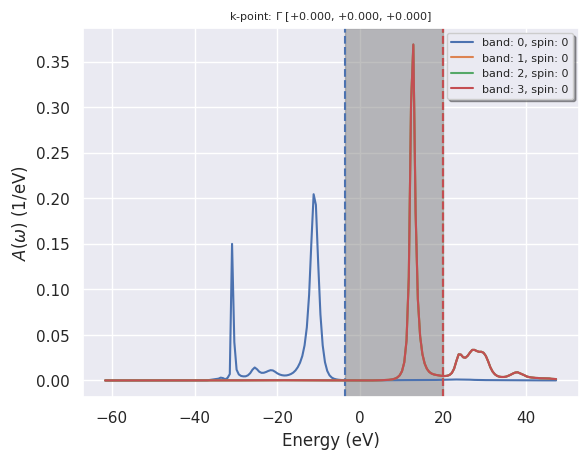
This example shows how to plot the \(G_0W_0\) spectral functions \(A(\omega)\) at the \(\Gamma\) point. See also lesson tgw2_4
with abilab.abiopen(abidata.ref_file("al_g0w0_sigmaw_SIGRES.nc")) as al_sigres:
# Plot A(w) for the first spin, the gamma point, and bands in [0,1,2,3]
al_sigres.plot_spectral_functions();
Analyzing multiple SIGRES files with robots#
To analyze the convergence of the QP results, we can use the SigresRobot. Let’s build our robot from a list of SIGRES files.
# List of SIGRES files computed with different values of nband.
filenames = [
"si_g0w0ppm_nband10_SIGRES.nc",
"si_g0w0ppm_nband20_SIGRES.nc",
"si_g0w0ppm_nband30_SIGRES.nc",
]
filepaths = [abidata.ref_file(fname) for fname in filenames]
robot = abilab.SigresRobot.from_files(filepaths)
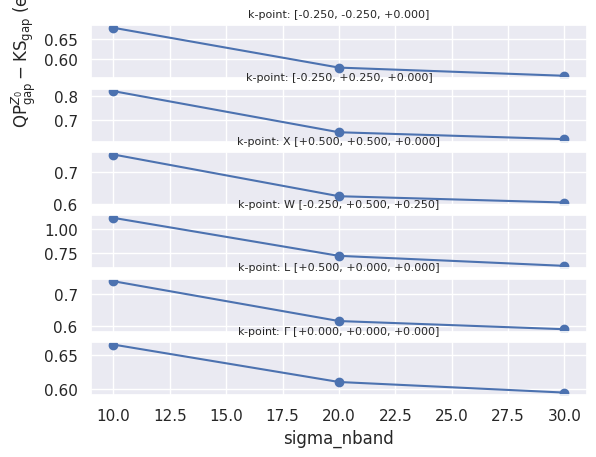
Then we plot the convergence of the QP direct gap as a function of the number of bands in the self-energy for all the k-points available in the netcdf files:
robot.plot_qpgaps_convergence(sortby="sigma_nband", sharey=False);
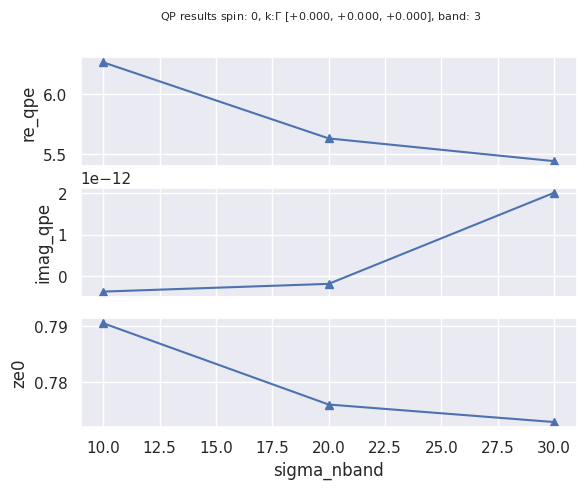
If we are interested in the convergence of the real/imaginary part of the self-energy and of the renormalization factor …
robot.plot_qpdata_conv_skb(spin=0, kpoint=(0, 0, 0), band=3, sortby="sigma_nband");
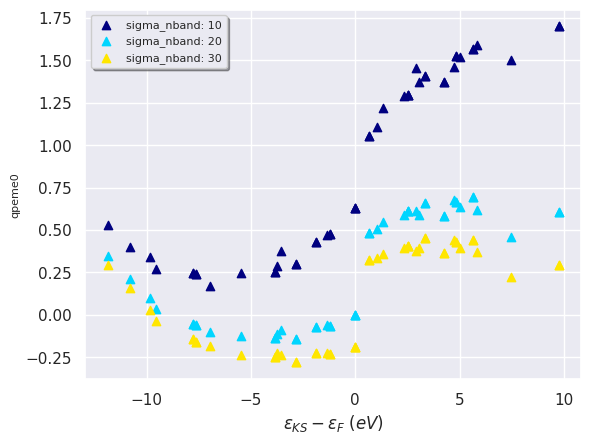
We can also plot the QP data as a function of the KS energies on the same figure with:
robot.plot_qpfield_vs_e0("qpeme0", sortby="sigma_nband");
#robot.get_qpgaps_dataframe(spin=0, kpoint=(0, 0, 0))

