Note
Go to the end to download the full example code.
Phonon convergence of ε∞, BECS, phonons and quadrupoles
This example shows how to use the DdbRobot to analyze the convergence of eps_inf, BECS, phonons and dynamical quadrupole with respect to the number of k-points.
import os
import abipy.data as abidata
Initialize the DdbRobot from a list of paths to DDB files Here we use DDB files shipped with the AbiPy package in data/refs/alas_eps_and_becs_vs_ngkpt Each DDB has been computed with a different k-mesh.
paths = ["AlAs_222k_DDB", "AlAs_444k_DDB","AlAs_666k_DDB", "AlAs_888k_DDB"]
paths = [os.path.join(abidata.dirpath, "refs", "alas_eps_and_becs_vs_ngkpt", f) for f in paths]
from abipy.dfpt.ddb import DdbRobot
ddb_robot = DdbRobot.from_files(paths)
Call anaddb to get ε∞ for all the DDB files. Results and metadata are stored in the epsinf_data.df dataframe.
epsinf_data = ddb_robot.anacompare_epsinf()
print("ε∞ dataframe:\n", epsinf_data.df)
epsinf_data.plot_conv("nkpt", abs_conv=0.1)
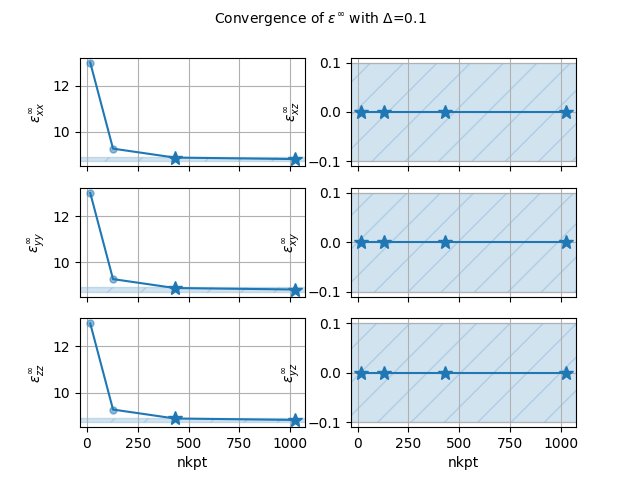
ε∞ dataframe:
xx yy zz yz xz xy formula chneut nkpt
0 12.996449 12.996449 12.996449 0.0 0.0 0.0 Al1 As1 1 16
1 9.268431 9.268431 9.268431 0.0 0.0 0.0 Al1 As1 1 128
2 8.881665 8.881665 8.881665 0.0 0.0 0.0 Al1 As1 1 432
3 8.818122 8.818122 8.818122 0.0 0.0 0.0 Al1 As1 1 1024
Call anaddb to get BECs for all the DDB files. Results and metadata are stored in the becs_data.df dataframe.
becs_data = ddb_robot.anacompare_becs()
print("BECS dataframe:\n", becs_data.df)
becs_data.plot_conv("nkpt", abs_conv=0.1)
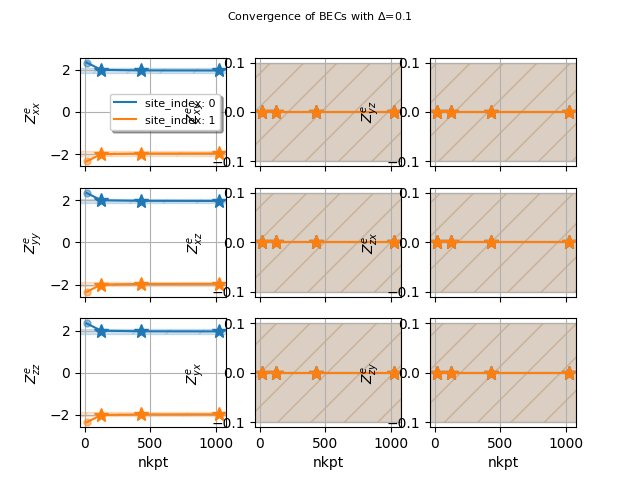
BECS dataframe:
element site_index frac_coords wyckoff ... zy formula chneut nkpt
0 Al 0 [0.0, 0.0, 0.0] 1a ... 0.0 Al1 As1 1 16
2 Al 0 [0.0, 0.0, 0.0] 1a ... 0.0 Al1 As1 1 128
6 Al 0 [0.0, 0.0, 0.0] 1a ... 0.0 Al1 As1 1 1024
4 Al 0 [0.0, 0.0, 0.0] 1a ... 0.0 Al1 As1 1 432
3 As 1 [0.25, 0.25, 0.25] 1d ... 0.0 Al1 As1 1 128
1 As 1 [0.25, 0.25, 0.25] 1d ... 0.0 Al1 As1 1 16
5 As 1 [0.25, 0.25, 0.25] 1d ... 0.0 Al1 As1 1 432
7 As 1 [0.25, 0.25, 0.25] 1d ... 0.0 Al1 As1 1 1024
[8 rows x 16 columns]
Call anaddb to get phonons at a single q-point for all the DDB files. Results and metadata are stored in the ph_data.ph_df dataframe.
ph_data = ddb_robot.get_phdata_at_qpoint(qpoint=(0, 0, 0))
print(ph_data.ph_df)
ph_data.plot_ph_conv("nkpt", abs_conv=0.1) # meV units.
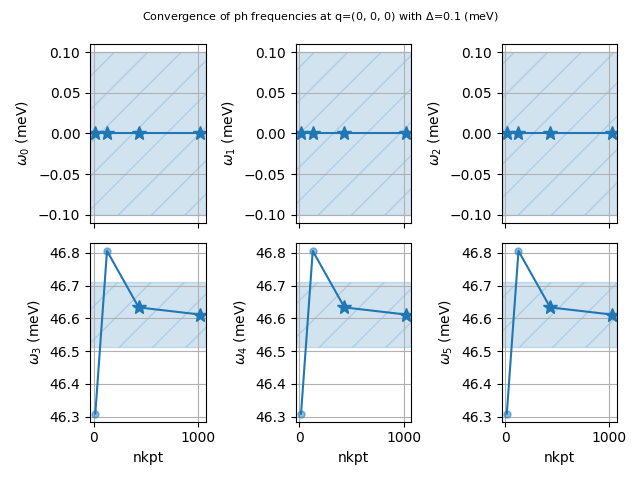
Calculation completed. Anaddb results available in: /tmp/tmptgzv9wkw
Calculation completed. Anaddb results available in: /tmp/tmpfzai8cuv
Calculation completed. Anaddb results available in: /tmp/tmped_gsnom
Calculation completed. Anaddb results available in: /tmp/tmpt5rgqo1e
mode0 ... spglib_lattice_type
../../data/refs/alas_eps_and_becs_vs_ngkpt/AlAs... 0.0 ... cubic
../../data/refs/alas_eps_and_becs_vs_ngkpt/AlAs... 0.0 ... cubic
../../data/refs/alas_eps_and_becs_vs_ngkpt/AlAs... 0.0 ... cubic
../../data/refs/alas_eps_and_becs_vs_ngkpt/AlAs... 0.0 ... cubic
[4 rows x 27 columns]
If the DDB contains dynamical quadrupoles, a similar dataframe with Q^* is automatically built and made available in ph_data.dyn_quad_df. A negative value of abs_conv is interpreted as relative convergence.
print(ph_data.dyn_quad_df)
ph_data.plot_dyn_quad_conv("nkpt", abs_conv=-0.02)
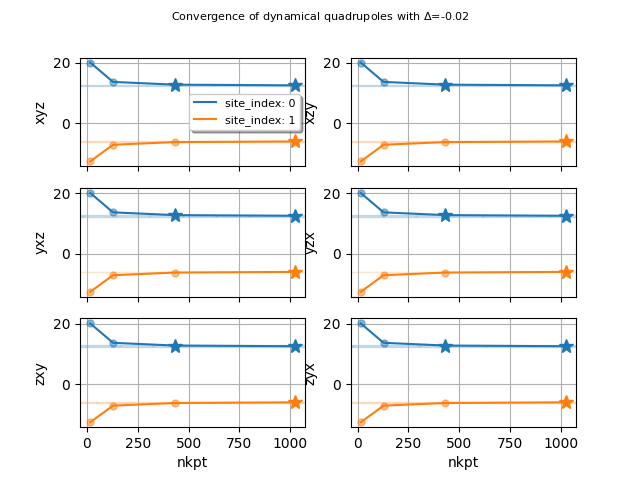
element site_index frac_coords wyckoff ... occopt ixc nband usepaw
0 Al 0 [0.0, 0.0, 0.0] 1a ... 1 1 4 0
1 As 1 [0.25, 0.25, 0.25] 1d ... 1 1 4 0
2 Al 0 [0.0, 0.0, 0.0] 1a ... 1 1 4 0
3 As 1 [0.25, 0.25, 0.25] 1d ... 1 1 4 0
4 Al 0 [0.0, 0.0, 0.0] 1a ... 1 1 4 0
5 As 1 [0.25, 0.25, 0.25] 1d ... 1 1 4 0
6 Al 0 [0.0, 0.0, 0.0] 1a ... 1 1 4 0
7 As 1 [0.25, 0.25, 0.25] 1d ... 1 1 4 0
[8 rows x 52 columns]
Total running time of the script: (0 minutes 7.905 seconds)